A* 알고리즘
A* 알고리즘
A* 알고리즘은 시작점에서 도착점까지의 최단 경로를 구하는 알고리즘이다. 그래프 뿐만 아니라 그래프로 변환할 수 있는(2차원 배열 등) 자료구조에서 전부 사용할 수 있다. 최단 경로라고 표현했지만, 문제에 따라 최소 가중치, 최소 비용등으로도 표현 가능하다.
A* 알고리즘에서 각각의 정점에 대한 평가 함수 f(x)는 g(x) + h(x)로 표현한다. g(x)는 시작점에서 현재 정점까지의 실제 경로 비용을, h(x)는 현재 정점에서 목표 정점까지의 예상 경로 비용을 나타낸다.
음수 간선이 없는 경우 일반적으로 g(x)는 다익스트라 알고리즘을 사용하고, h(x)는 맨해튼 거리, 유클리드 거리 등을 통해 예상 경로 비용을 계산하는 휴리스틱 함수를 사용한다. 다익스트라 알고리즘을 모든 x에 대하여 h(x)의 값이 0인 A* 알고리즘이라고 볼 수도 있다.
A* 알고리즘은 휴리스틱 기법을 사용하므로 항상 최적해를 반환하지는 않지만, 대부분의 경우 최적해 또는 최적해의 근사값을 반환한다.
9-Puzzle
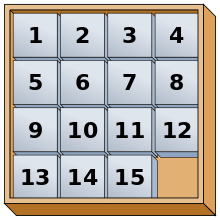
√(N + 1) * √(N + 1) 크기의 격자에 1 ~ N까지의 자연수와 빈 칸 하나가 들어있는 슬라이딩 퍼즐을 N-Puzzle이라고 부른다. 무작위로 배열된 초기 상태의 퍼즐을 목표 상태로 만들면 된다.
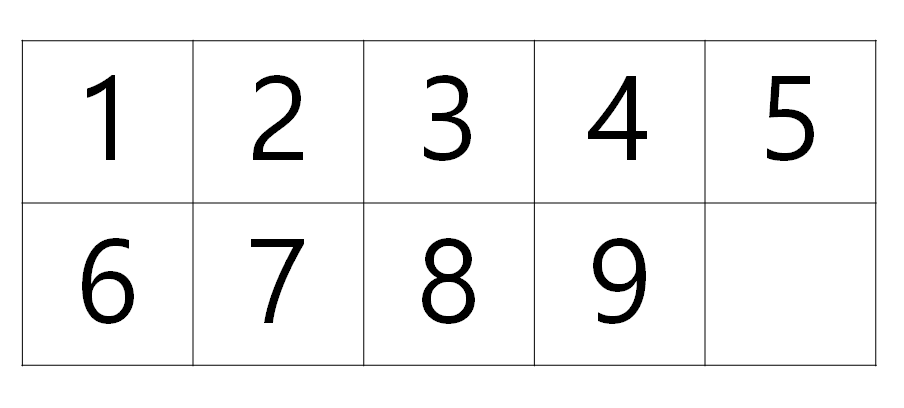
동일한 방식의 퍼즐을 2 * 5 크기의 격자에 만든 것을 9-Puzzle이라고 하고(실제로 존재하는 퍼즐은 아니다), A* 알고리즘을 통해서 풀어볼 것이다.
Solvability
용어 정리
순열(Permutation)
9-Puzzle의 1행 1열부터 2행 5열까지의 숫자를 나열한 것반전(Inversion)
임의의 순열 σ:{1, 2, …, n} → {1, 2, …, n}에 대해, i < j이고 σ(i) > σ(j)인 n 이하의 자연수 i, j의 순서쌍 (i, j)의 개수전치(Transposition)
순열에서 두 원소를 교환하는 연산. (a b)로 표현한다.N-cycle
(a b c)는 a → b, b → c, c → a로 순환하는 것을 의미하며, N은 cycle에 포함된 원소의 개수이다. 전치의 곱(합성)으로 표현할 수 있다.홀짝성(Parity)
순열에서 반전의 개수 혹은 전치의 곱으로 표현할 때 사용된 전치의 개수. 두 경우의 홀짝성은 항상 같다.홀순열/짝순열
Parity가 홀수인 순열을 홀순열(기순열), 짝수인 순열을 짝순열(우순열)이라고 한다.
본문
목표 상태의 parity는 짝수이다.
목표 상태를 순열로 표현하면 (1, 2, 3, 4, 5, 6, 7, 8, 9) 이다. 이 때 순열의 inversion parity는 0으로, 목표 상태는 짝순열이다.- 타일의 이동 후에도 순열의 parity는 항상 유지된다.
수평 이동
수평 이동은 순열의 원소 하나를 단순히 왼쪽 혹은 오른쪽으로 한 칸 옮기는 것이므로, 순열의 parity에는 변화가 없다.수직 이동
9-Puzzle에서의 수직 이동은 순열의 5-cycle로 표현할 수 있다. 예를 들어, 목표 상태에서 5번 타일을 한 칸 아래로 내리면 순열은 (1, 2, 3, 4, 6, 7, 8, 9, 5)가 되고, 이전 상태와 비교했을 때 (5 6 7 8 9)의 5-cycle이 형성된다.5-cycle 분해
5-cycle은 다음과 같이 4개의 전치로 분해할 수 있다(a b c d e) = (a e)(a d)(a c)(a b)
따라서, 수직 이동 = (수직 이동 이전 전치의 함성( = 짝수))(4개의 전치(= 짝수))로 표현할 수 있고, 전치의 총 개수는 짝수를 유지하므로 순열의 parity에는 변화가 없다.
- 결론
타일의 이동 순서와 방향에 관계 없이 순열의 parity는 항상 처음과 같다. 따라서, 초기 상태의 parity가 홀수라면 절대 목표 상태로 만들 수 없다.
참고로 퍼즐의 열의 개수가 짝수인 경우, 수직 연산이 N-cycle(N은 짝수)로 표현된다. N이 짝수인 경우 N-cycle은 홀수 개의 전치로 표현할 수 있으므로 수직 이동시 parity가 바뀐다. 따라서 solvability를 판단할 때 빈 칸의 행도 고려해야 한다.
그렇다면 초기 상태의 parity가 짝수인 모든 퍼즐은 목표 상태로 만들 수 있는가?도 증명해야 한다. 8-Puzzle의 경우는 교대군 An이 3-cycle의 곱으로 표현될 수 있음을 이용하여 증명되었으나(이해 못함), 9-Puzzle은 연산이 3-cycle이 아니라 5-cycle로 표현되어 명확하지 않다. 그냥 적당히 큰 n에서는 잘 작동할 것이라는 믿음을 가지고 구현했다.
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
#include <bits/stdc++.h>
#define FastIO ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define R 2
#define C 5
using namespace std;
unordered_map<string, int> dist; // start에서 각 상태까지의 거리를 저장하는 map { permutation, distance }
unordered_map<string, string> prev_state; // 이전 상태의 순열을 저장하는 map { cur_permutation, prev_permutation }
string start; // 퍼즐의 시작 상태(string 형태의 순열로 표현)
string goal = "123456789_"; // 퍼즐의 목표 상태
// 상, 우, 하, 좌로 이동
int dr[4] = {0, 1, 0, -1};
int dc[4] = {-1, 0, 1, 0};
// 같은 시작 상태에 대해서 A*로 한 번, 다익스트라로 한 번 실행.
bool dijkstra = false;
int a_star_count, dijkstra_count;
int a_star_time, dijkstra_time;
// 모든 타일의 맨해튼 거리를 사용해서 h(x) 계산
int CalcHx(string p) {
int hx = 0;
if (dijkstra) {
return hx;
}
for (int i = 0; i < p.size(); i++) {
int goal_idx = goal.find(p[i]);
int r1 = i / C;
int c1 = i % C;
int r2 = goal_idx / C;
int c2 = goal_idx % C;
hx += abs(r1 - r2) + abs(c1 - c2);
}
return hx;
}
// A*, 다익스트라 알고리즘 종료 후 각각의 swap count와 소요 시간 출력
void PrintResult() {
cout << "A* Swap Count = " << a_star_count << '\n';
cout << "A* Time = " << a_star_time << "\n\n";
cout << "Dijkstra Swap Count = " << dijkstra_count << '\n';
cout << "Dijkstra Time = " << dijkstra_time << "\n\n";
}
// 시작 상태에서 목표 상태까지의 진행 과정 출력
void PrintSolutionSteps(int gx, string cur ,string prev) {
stack<string> s;
prev_state[cur] = prev;
while (prev_state[cur] != "start") {
s.push(cur);
cur = prev_state[cur];
}
s.push(start);
if (!dijkstra) {
cout << "========================= A* Steps =========================" << '\n';
a_star_count = gx + 1;
}
else {
cout << "========================= Dijkstra Steps =========================" << '\n';
dijkstra_count = gx + 1;
}
while (!s.empty()) {
cur = s.top();
s.pop();
for (int i = 0; i < R; i++) {
for (int j = 0; j < C; j++) {
cout << cur[i * C + j] << " ";
}
cout << '\n';
}
cout << '\n';
}
}
// 퍼즐의 빈 칸을 인접한 상, 하, 좌, 우 중 한 칸으로 swap
void MoveBlank(int gx, string p, priority_queue<tuple<int, int, string>>& pq) {
// 순열에서 빈칸의 index를 통해 퍼즐에서의 행, 열 계산
int blank_idx = p.find('_');
int r = blank_idx / C;
int c = blank_idx % C;
for (int i = 0; i < 4; i++) {
int nr = r + dr[i];
int nc = c + dc[i];
// 인접한 상하좌우로 이동했을 때 퍼즐 밖으로 나가는 경우는 이동하지 않음
if (nr < 0 || nr >= R || nc < 0 || nc >= C) {
continue;
}
// 타일이 이동한 결과를 move_p에 저장
string move_p = p;
int swap_idx = nr * C + nc;
swap(move_p[blank_idx], move_p[swap_idx]);
// 목표 상태에 도달한 경우, 해결 과정을 출력하고 함수 종료
if (move_p == goal) {
PrintSolutionSteps(gx, move_p ,p);
break;
}
// 이전에 도달한 적 없는 상태인 경우에만 priority queue에 push
if (dist.find(move_p) == dist.end()) {
dist[move_p] = gx + 1;
prev_state[move_p] = p;
pq.push({-(gx + 1 + CalcHx(move_p)), gx + 1, move_p});
}
}
}
// 시작 상태에서 목표 상태까지의 거리를 계산
void CalcDistance() {
priority_queue<tuple<int, int, string>> pq; // { -f(x), g(x), permutation } f(x)를 기준으로 오름차순 정렬
dist[start] = 0;
prev_state[start] = "start";
pq.push({0 + CalcHx(start), 0, start});
while (!pq.empty()) {
int gx = get<1>(pq.top());
string p = get<2>(pq.top());
pq.pop();
MoveBlank(gx, p, pq);
// 목표 상태에 도달한 경우 함수 종료
if (prev_state.find(goal) != prev_state.end()) {
break;
}
}
}
// inversion count를 계산
int CalcInversionCount(string p) {
int inversions = 0;
for (int i = 0; i < p.size(); i++) {
for (int j = i + 1; j < p.size(); j++) {
if (p[i] > p[j]) {
inversions++;
}
}
}
return inversions;
}
// 랜덤한 시작 상태를 만드는 함수
void InitStartState() {
random_device rd;
mt19937 g(rd());
vector v = {'1', '2', '3', '4', '5', '6', '7', '8', '9'};
while(1) {
shuffle(v.begin(), v.end(), g);
string permutation(v.begin(), v.end());
// 시작 상태의 inversion parity가 짝수인 경우에만 퍼즐을 풀 수 있음
if(CalcInversionCount(permutation) % 2 == 0) {
start = permutation.insert(g() % (permutation.size() + 1), 1, '_');
break;
}
}
}
void Init() {
dist.clear();
prev_state.clear();
dijkstra = !dijkstra;
}
int main() {
FastIO;
for (int i = 0; i < 2; i++) {
if (!dijkstra) {
InitStartState();
}
// 목표 경로까지의 거리를 구하는 시간 계산
auto start = chrono::high_resolution_clock::now();
CalcDistance();
auto end = chrono::high_resolution_clock::now();
if (dijkstra) {
dijkstra_time = chrono::duration_cast<chrono::duration<double>>(end - start).count();
PrintResult();
}
else {
a_star_time = chrono::duration_cast<chrono::duration<double>>(end - start).count();
}
Init();
}
}
GCC 컴파일러가 없는 경우 코드는 여기서 실행할 수 있다.
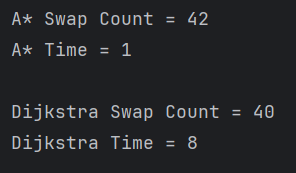
결론
일반적으로 A* 알고리즘은 다익스트라 알고리즘에 비해 시간은 빠르지만 최적해를 찾아내는 비율이 낮다는 것을 알 수 있다.
참고 자료
Parity of a permutation
Alternating Group is Generated by 3-Cycles
The Fifteen Puzzle A Motivating Example for the Alternating Group
An is generated by the 3-cycles