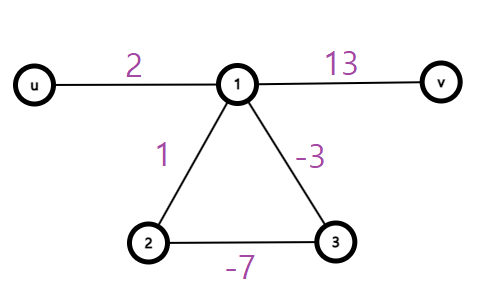
벨만-포드(Bellman-Ford)
벨만-포드 알고리즘
벨만-포드 알고리즘은 다익스트라 알고리즘과 마찬가지로 한 정점에서 다른 모든 정점까지의 최단 거리를 구하는 알고리즘이다.
다익스트라 알고리즘은 음수 간선이 포함된 경우 제대로 동작하지 않지만, 벨만-포드 알고리즘은 음수 간선이 포함된 경우에도 정확한 최단 거리를 구할 수 있고, 음수 사이클의 존재 여부까지 판별할 수 있다.
진행 방식
- 시작 정점에서 도달한 적 있는 정점에 연결된 모든 간선에 대해 최신화를 진행한다.
- 1번을 (정점의 개수 - 1)번 반복한다.
정점의 개수가 N개인 그래프의 최단 경로에는 최대 N - 1개의 간선이 포함될 수 있다. 그렇기 때문에 N - 1번 루프를 돌면서 시작점에서 k (1 ≤ k ≤ N - 1)개의 간선을 거쳐서 도달할 수 있는 정점의 최단 거리를 최신화하면 된다.
엄밀한 증명이나 완화같은 내용은 생략. (나중에 추가할 수도 있음)
음수 사이클 판별
N개의 정점으로 구성된 그래프가 있을 때, 임의의 노드 u, v사이의 최단 경로가 있다고 가정하자. 이 때 이 경로는 최대 몇 개의 간선으로 구성될 수 있을까?
답은 u와 v 사이에 다른 정점들이 전부 들어가 있는 경우로, 최대 N - 1개의 간선으로 구성될 수 있다. 그렇다면 최단 경로에 포함된 간선이 N개 이상이라는 것은 무슨 의미일까.
최단 경로에 포함된 간선이 N개 이상이라는 뜻은 이미 방문한 정점을 또 방문했을 때 최단 경로가 감소한다는 것을 의미한다. 해당 정점을 방문할때마다 최단 경로가 줄어들게 되고, 결국 -INF가 된다.
벨만-포드 알고리즘은 N - 1번 루프를 돈다. 이후에 한 번 더 최신화를 했을 때, 최단 경로가 감소한 정점이 있다면 음수 사이클이 존재한다는 뜻이다.
구현
11657번: 타임머신의 코드이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <bits/stdc++.h>
#include <ext/rope>
#define FastIO ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define ll long long
#define INF 101010101010
using namespace std;
using namespace __gnu_cxx;
int N, M;
ll dist[500];
vector<pair<int, ll>> graph[500];
void Output() {
for(int i = 1; i < N; i++) {
if(dist[i] == INF) {
cout << "-1" << '\n';
}
else {
cout << dist[i] << '\n';
}
}
}
void Solve() {
dist[0] = 0;
for(int i = 1; i < N; i++) {
dist[i] = INF;
}
for(int i = 0; i < N; i++) {
for(int cur = 0; cur < N; cur++) {
for(pair<int, ll> n : graph[cur]) {
int nxt = n.first;
ll w = n.second;
if(dist[cur] != INF && dist[nxt] > dist[cur] + w) {
// 음수 사이클 판별
if(i == N - 1) {
cout << "-1";
exit(0);
}
dist[nxt] = dist[cur] + w;
}
}
}
}
}
void Input() {
cin >> N >> M;
for(int i = 0; i < M; i++) {
int A, B;
ll C;
cin >> A >> B >> C;
graph[A - 1].push_back({B - 1, C});
}
}
int main() {
FastIO;
Input();
Solve();
Output();
}
시간 복잡도
정점의 개수를 $|V|$, 간선의 개수를 $|E|$개라고 할 때, 사이클 탐지를 한다면 $|V|$번, 아니라면 $|V - 1|$번 루프를 돌게 된다. 이 때 루프 한 번당 $|E|$번 최신화를 하므로 시간 복잡도는 $O(|V| * |E|)$이다.
SPFA(Shortest Path Faster Algorithm)
벨만-포드의 발전된 형태로 SPFA 알고리즘이 있다. 벨만-포드 알고리즘은 루프마다 모든 정점에 연결된 간선에 대해 최신화를 진행하지만, SPFA 알고리즘은 큐를 사용하여 최신화 된 정점에 연결된 간선에 대해서만 최신화를 진행한다.
구현
위의 11657번: 타임머신을 SPFA로 구현한 코드이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <bits/stdc++.h>
#include <ext/rope>
#define FastIO ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define ll long long
#define INF 101010101010
using namespace std;
using namespace __gnu_cxx;
int N, M;
ll dist[500];
int visited[500];
bool inQueue[500];
vector<pair<int, ll>> graph[500];
void Output() {
for(int i = 1; i < N; i++) {
if(dist[i] == INF) {
cout << "-1" << '\n';
}
else {
cout << dist[i] << '\n';
}
}
}
void Solve() {
dist[0] = 0;
for(int i = 1; i < N; i++) {
dist[i] = INF;
}
queue<int> q;
q.push(0);
visited[0]++;
inQueue[0] = true;
while(!q.empty()) {
int cur = q.front();
inQueue[cur] = false;
q.pop();
for(pair<int, ll> n : graph[cur]) {
int nxt = n.first;
ll w = n.second;
if(dist[nxt] > dist[cur] + w) {
dist[nxt] = dist[cur] + w;
if(!inQueue[nxt]) {
inQueue[nxt] = true;
q.push(nxt);
if(++visited[nxt] > N - 1) {
cout << "-1";
exit(0);
}
}
}
}
}
}
void Input() {
cin >> N >> M;
for(int i = 0; i < M; i++) {
int A, B;
ll C;
cin >> A >> B >> C;
graph[A - 1].push_back({B - 1, C});
}
}
int main() {
FastIO;
Input();
Solve();
Output();
}
!inQueue[nxt]인 경우에 ++visited[nxt]를 하는 이유
개인적으로 헷갈렸던 부분이다. 최단 경로가 갱신될 때마다 ++visited[nxt]를 하는 것이 아니라, 최단 경로가 갱신되고, 큐에 들어있지 않을 때 ++visited[nxt]를 한다. 이유가 뭘까?
우선 임의의 정점이 큐에 들어간다는 게 무슨 의미일까? 해당 정점까지의 최단 경로가 갱신되었다는 뜻이다. 최단 경로가 (정점의 개수 - 1)번 이상 갱신될 수 있을까? 당연히 없다. 따라서 사이클이 없는 경우, 임의의 정점이 큐에 들어가는 최대 횟수는 (정점의 개수 - 1)번 이라는 것을 알 수 있다.
그렇다면 왜 꼭 큐에 들어가는 경우에만 ++visited[nxt]를 해야 하는 것일까? 큐에 들어가지 않고 최단 경로가 갱신되는 경우, k번째 간선을 이용한 최단 거리 갱신인지 k + 1번째 간선을 이용한 최단 거리 갱신인지 알 수 없다. k번째 간선을 이용해서 최단 거리 갱신이 2번 된 경우, visited[nxt] += 2가 되지만, 사실 ++visited[nxt]가 되어야 한다.
visited[nxt] = i의 의미가 nxt 정점의 최단 경로가 i번 갱신되었다가 아니라 nxt 정점의 최단 경로가 i번째 간선까지 사용해서 갱신되었다라고 생각하면 이해하기 편하다.
정리하면, 단순히 최단 경로가 갱신될 때마다 ++visited[nxt] 연산을 하면 사이클이 없는데 사이클이 있다고 판단하는 경우가 생길 수 있다. 하지만 큐에 들어갈때마다 ++visited[nxt] 연산을 하면, 사이클에 포함되는 정점이 큐에 INF번 들어가게 되므로 일정 횟수 내에 항상 탐지할 수 있다.
시간 복잡도
SPFA의 평균적인 시간 복잡도는 $O(|E|)$지만, 최악의 경우 $O(|V| * |E|)$로 벨만-포드보다 느린 경우도 있을 수 있다.