너비 우선 탐색(BFS)

너비 우선 탐색(BFS: Breadth First Search)

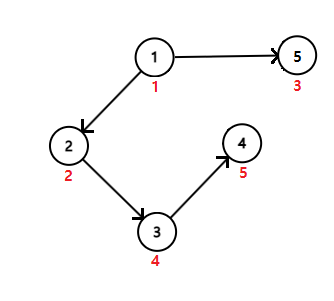
BFS는 너비를 우선적으로 탐색하는 알고리즘으로 그래프 뿐만 아니라 트리, 배열 등에서도 사용할 수 있다. 진행 방식은 아래와 같다. 그래프와 트리에서는 정점으로, 배열에서는 칸으로 생각하면 된다.

1. 시작 정점을 방문한다.
2. 시작 정점과 연결된 정점을 전부 방문한다.
3. 2번에서 방문한 정점들을 시작 정점으로 탐색을 진행한다.

모든 정점을 방문할때까지 1~3번 과정을 반복하면 된다. 위 그래프에서 BFS를 진행하면 1->2->5->3->4의 순서대로 그래프를 탐색하게 된다. 2번 정점 대신 5번 정점을 먼저 방문해도 상관없다. BFS는 큐를 사용하여 구현할 수 있다.

---

BFS의 시간 복잡도

정의
$\left\vert V \right\vert$: 정점의 개수
$\left\vert E \right\vert$: 간선의 개수

DFS의 시간 복잡도와 동일하다.

인접 리스트로 구현한 그래프에서 dfs를 진행한다고 생각해보자. 우선 모든 정점을 한 번씩 방문해야 하므로 정점 방문의 시간 복잡도는 $O(\left\vert V \right\vert)$이다. 정점을 방문하는 과정에서 유향 그래프의 경우는 한 번, 무향 그래프의 경우에는 두 번씩 간선을 탐색해야 하므로 시간 복잡도는 $O(\left\vert E \right\vert)$이다. 따라서 최종적인 시간 복잡도는 $O(\left\vert V \right\vert + \left\vert E \right\vert)$이다.

인접 행렬로 구현한 그래프도 똑같다. 하지만 인접 행렬 특성상 $V^2$개의 행렬을 탐색해야 하므로 시간 복잡도는 $O(\left\vert V \right\vert^2)$이다.

---

문제

1260번: DFS와 BFS에서 BFS만 구현한 코드다.

#include <bits/stdc++.h>
#define FastIO ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define pb push_back
using namespace std;

int N, M, V;
vector<int> graph[1001];
bool visited[1001];


void Bfs(int cur_node) {
    queue<int> q;
    q.push(cur_node);
    visited[cur_node] = true;
    cout << cur_node << " ";

    while(!q.empty()) {
        cur_node = q.front();
        q.pop();

        for(int nxt_node : graph[cur_node]) {
            if(visited[nxt_node]) {
                continue;
            }

            q.push(nxt_node);
            visited[nxt_node] = true;
            cout << nxt_node << " ";
        }
    }
}


void Solve() {
    Bfs(V);
}


void Input() {
    cin >> N >> M >> V;

    for(int i = 0; i < M; i++) {
        int u, v;
        cin >> u >> v;

        graph[u].pb(v);
        graph[v].pb(u);
    }

    for(int i = 1; i <= N; i++) {
        sort(graph[i].begin(), graph[i].end());
    }
}


int main() {
    FastIO;

    Input();
    Solve();
}