다익스트라(Dijkstra)
다익스트라 알고리즘
다익스트라 알고리즘은 한 정점에서 다른 모든 정점까지의 최단 경로를 구하는 알고리즘이다. 그래프 뿐만 아니라 그래프로 변환할 수 있는(2차원 배열 등) 자료구조에서 전부 사용할 수 있다. 최단 경로라고 표현했지만, 문제에 따라 최소 가중치, 최소 비용등으로도 표현 가능하다.
진행 방식
- 방문하지 않은(거리가 확정되지 않은) 정점 중 가장 가까운 정점을 방문한다(거리를 확정한다).
- 선택한 정점과 인접한 정점의 거리를 최신화한다.
- 모든 정점에 방문할 때까지 1, 2번을 반복한다.
핵심은 방문과 최신화다. 이 둘이 다르다는 것을 생각하면서 아래 예시를 보자
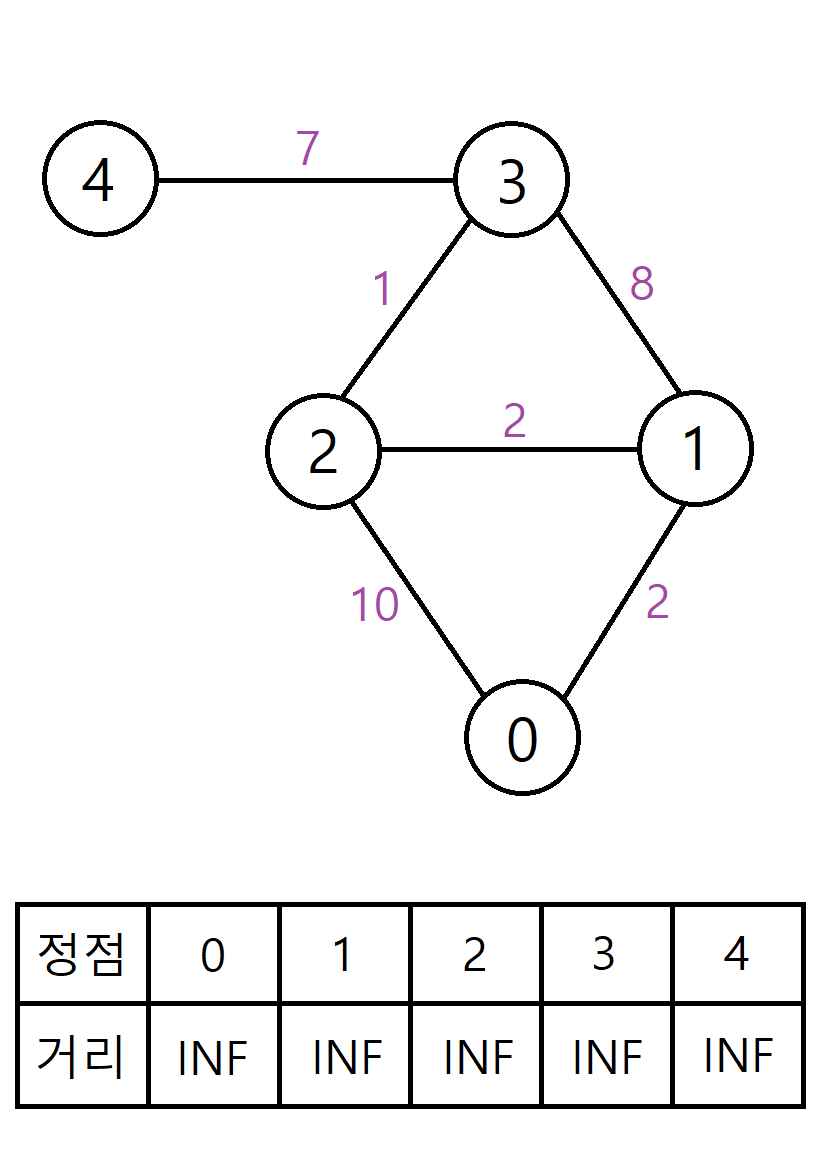
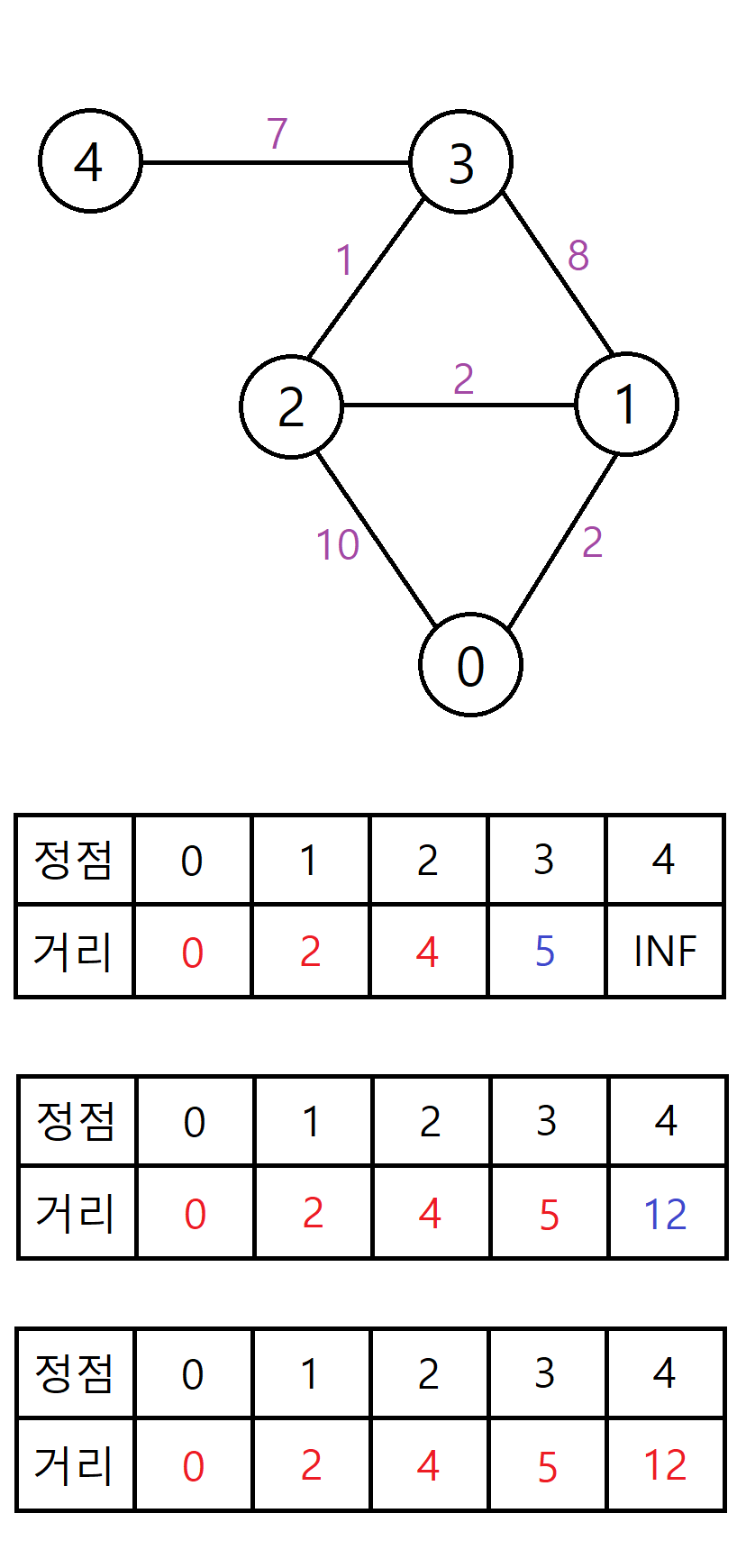
위와 같은 그래프에서 다익스트라 알고리즘을 수행한다고 생각해보자. 간선 옆의 보라색 글씨가 간선의 거리고, 시작점은 0번 정점이라고 가정한다.
밑의 테이블은 현재 단계에서, 0번 정점에서 해당 정점까지의 최단 거리이다. 방문한 상태, 즉 거리가 확정된 상태는 빨간색 , 단순 최신화만 된 상태는 파란색 이다.
모든 최단 거리 테이블의 초기값은 INF이다. INF는 현재 문제에서 나올 수 있는 최단 거리의 최댓값보다 큰 임의의 값으로, 문제마다 다르게 설정할 수 있다.
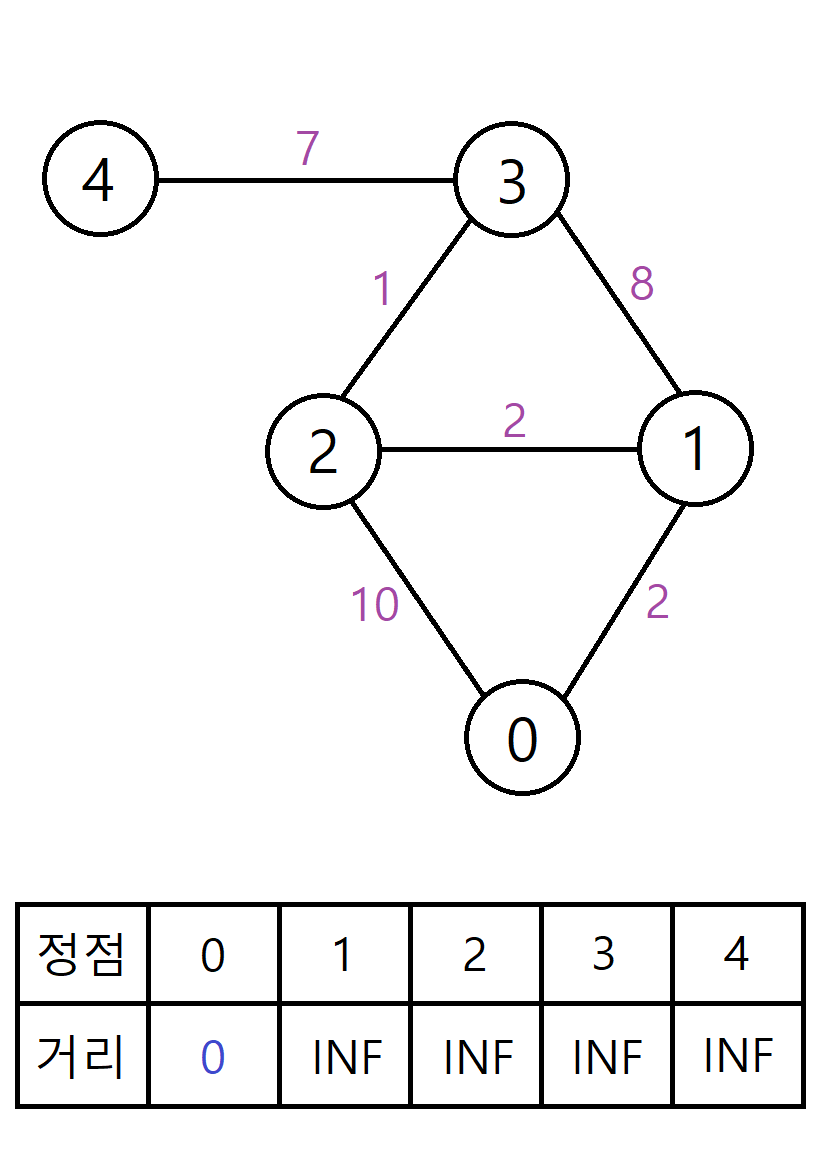
시작점이 0번 정점이므로 0번 정점까지의 최단 거리를 0으로 최신화한다(self loop).
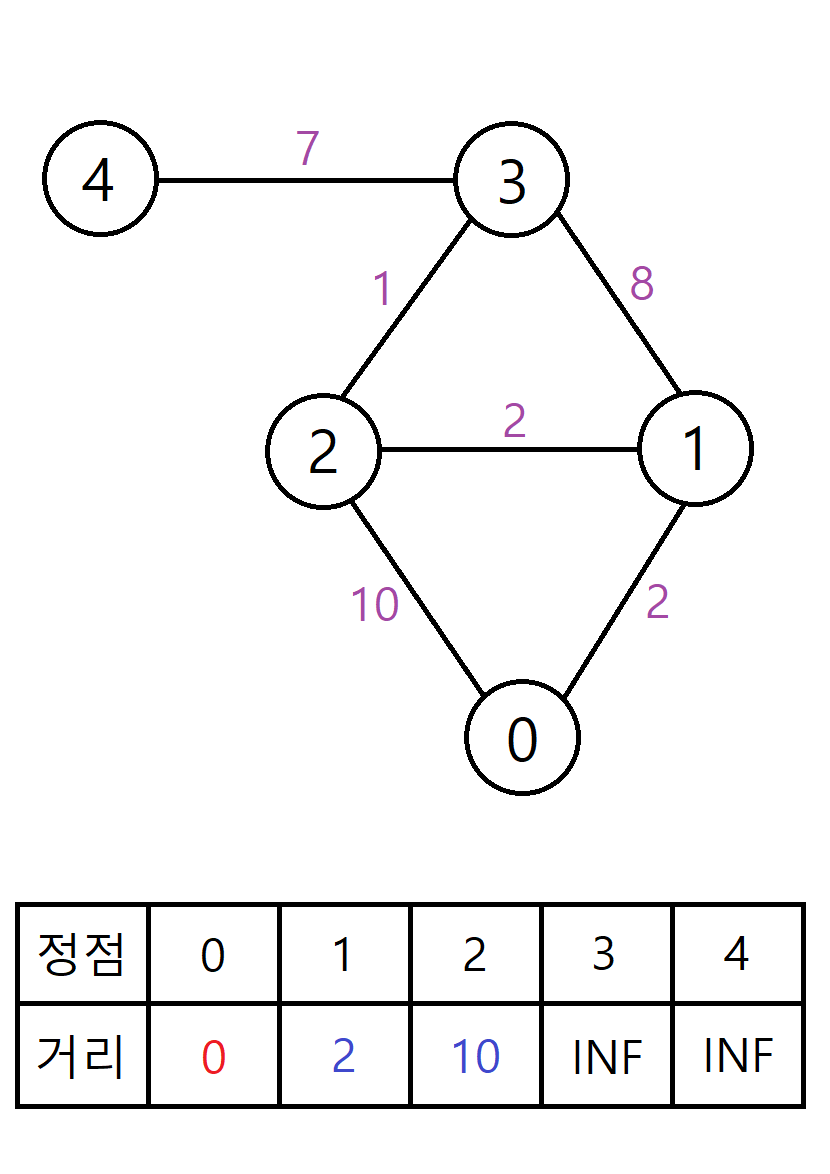
현재 거리가 최신화 된 정점 중 가장 가까운 정점이 0번 정점이므로, 0번 정점을 방문하고 거리를 확정한다.
이후 0번 정점과 인접한 1번, 2번 정점의 최단 거리를 각각 2, 10으로 최신화한다.
현재 거리가 최신화 된 정점 중 가장 가까운 정점이 1번 정점이므로, 1번 정점을 방문하고 거리를 확정한다.
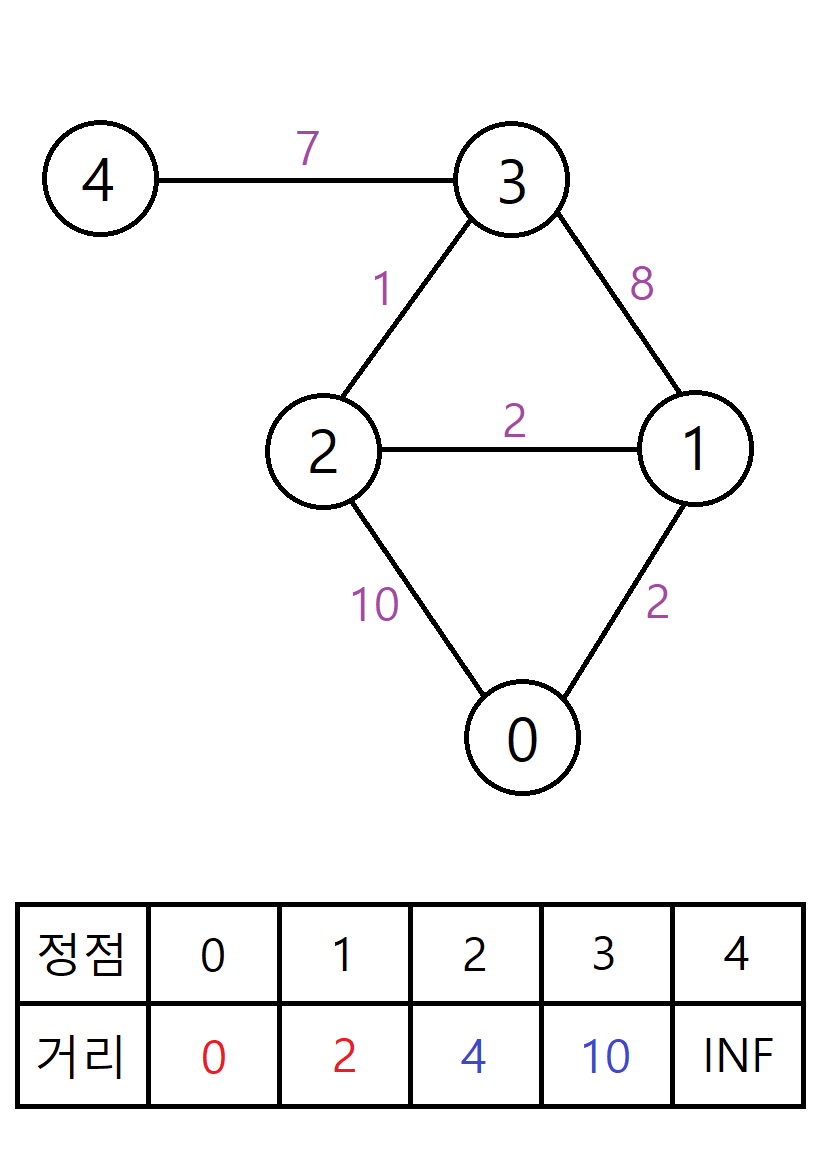
이후 1번 정점과 인접한 2번, 3번 정점의 최단 거리를 각각 4, 10으로 최신화한다. 0번 정점과도 인접해있지만, 0번 정점은 이미 방문한 상태이므로 최신화하지 않는다. 또한 2번 정점은 이전 단계에서 최신화하긴 했지만 이전 단계의 최단 거리보다 현재 단계의 최단 거리가 더 작으므로 새롭게 최신화해준다.
알고리즘 진행 단계에 따른 테이블 변화이다. 마지막 4번 정점까지 방문을 마친 후 알고리즘을 종료하면 된다.
현재 최신화된 최단 거리 중 가장 짧은 정점을 방문하는 것은 그리디, memoization을 통해 이전 단계의 최단 거리를 활용하는 것은 dp이다. 즉 다익스트라 알고리즘은 그리디와 dp의 특성을 모두 가지고 있다.
주의 사항
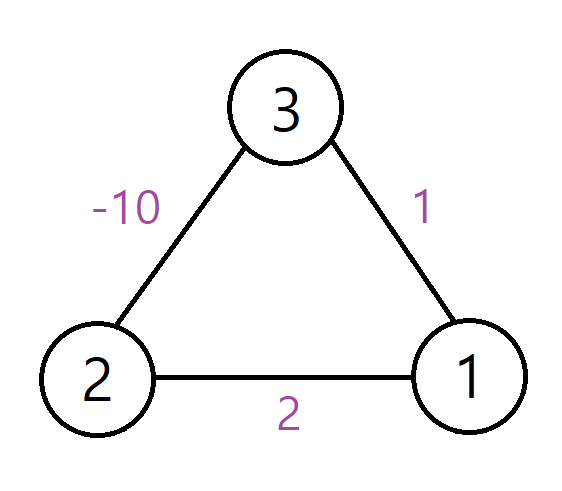
다익스트라 알고리즘은 음수 간선을 가지는 그래프에서는 사용할 수 없다. 한 번 방문한 정점은 다시 방문하지 않는 게 다익스트라 알고리즘의 기본 원칙인데, 음수 간선이 있으면 이미 방문한 정점을 다른 정점을 경유해서 다시 방문하는 게 최단 거리인 경우가 있기 때문이다.
위 그래프에서 1번 정점을 시작으로 다익스트라 알고리즘을 적용하면 1번 정점 방문 후, 3번 정점을 방문하게 된다. 이 때 3번 정점의 거리는 1로 결정되지만, 2번 정점을 경유해서 3번 정점을 방문하면 거리가 -8이 된다.
음수 간선이 있는 경우, 벨만-포드 알고리즘 또는 플로이드-워셜 알고리즘을 사용해야 정확한 최단 거리를 구할 수 있다.
구현
5972번: 택배 배송의 코드이다. 일반적으로 우선순위 큐를 사용하여 구현한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include <bits/stdc++.h>
#define FastIO ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define INF 1010101010
using namespace std;
int N, M;
int dist[50001]; // 최단 거리 저장
int visited[50001]; // 방문 여부 체크
vector<pair<int, int>> graph[50001]; // {node, dist}
void Output() {
cout << dist[N];
}
void Solve() {
// 최신화 한 노드들 큐에 push
priority_queue<pair<int, int>> pq; // {dist, node}
pq.push({0, 1});
dist[1] = 0;
while(!pq.empty()) {
int cur = pq.top().second;
// 큐에서 pop -> 노드 방문
pq.pop();
// 이미 방문한 노드 재방문 X
if(visited[cur]) {
continue;
}
visited[cur] = true;
for(int i = 0; i < graph[cur].size(); i++) {
int nxt = graph[cur][i].first;
int w = graph[cur][i].second;
if(visited[nxt]) {
continue;
}
// 최단 거리가 최신화 되는 경우에만 큐에 push
if(dist[nxt] > dist[cur] + w) {
dist[nxt] = dist[cur] + w;
// 우선순위 큐는 기본적으로 내림차순이기 때문에, -dist를 push
pq.push({-dist[nxt], nxt});
}
}
}
}
void Input() {
cin >> N >> M;
for(int i = 0; i < M; i++) {
int u, v, d;
cin >> u >> v >> d;
// 그래프 초기화
graph[u].push_back({v, d});
graph[v].push_back({u, d});
}
// dist INF로 초기화
for(int i = 1; i <= N; i++) {
dist[i] = INF;
}
}
int main() {
FastIO;
Input();
Solve();
Output();
}
시간 복잡도
우선순위 큐를 사용하지 않고 브루트 포스로 구현하면 한 정점을 방문할 때마다 인접한 모든 정점의 최단 거리를 최신화 하고, 최솟값을 찾아야 하기 때문에 $O(V^2)$의 시간 복잡도를 가진다.
우선순위 큐를 사용하면 $E$개의 간선을 확인하는 과정에서 $O(logE)$의 시간 복잡도로 현재 단계의 최단 거리를 찾을 수 있기 때문에 $O(ElogE)$의 시간 복잡도를 가진다.