그리디(Greedy)

그리디

그리디 알고리즘은 현재 상황에서 가장 좋은(최적의) 선택을 하는 알고리즘 기법이다. 부분 문제들의 최적해의 집합이 전체 문제의 최적해와 일치할 때만 사용할 수 있다.

---

부분 문제들의 최적해의 집합이 전체 문제의 최적해와 일치

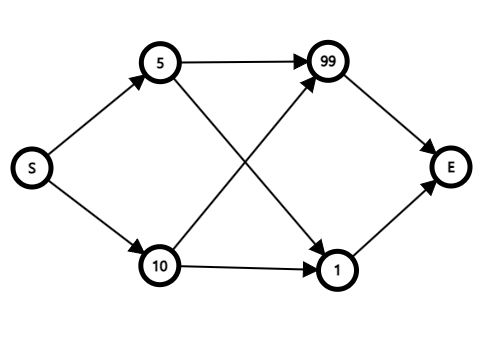
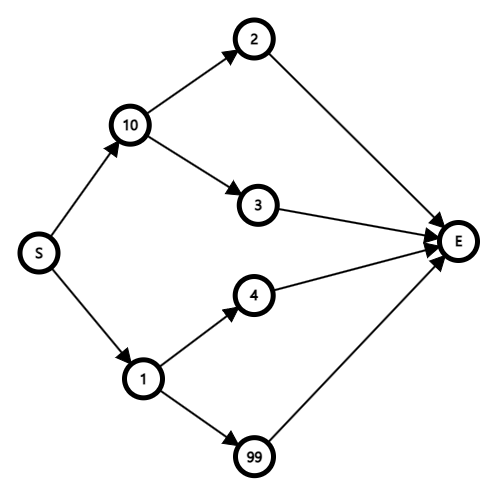
노드에 적힌 숫자의 합을 최대로 해서 S에서 E까지 가는 문제가 있다고 해보자. 위 그래프에서는 2개의 부분 문제가 나올 수 있다.

1. S에서 5 또는 10으로 가는 문제
2. 1번에서 선택된 노드에서 99 또는 1로 가는 문제

2번에서 선택된 노드에서 E로 가는 것은 경우의 수가 항상 하나밖에 없어서 결과에 영향을 미치지 않으므로 포함시키지 않았다. 각 문제의 최적해를 구해보고 전체 문제의 최적해와 비교해보자.

---

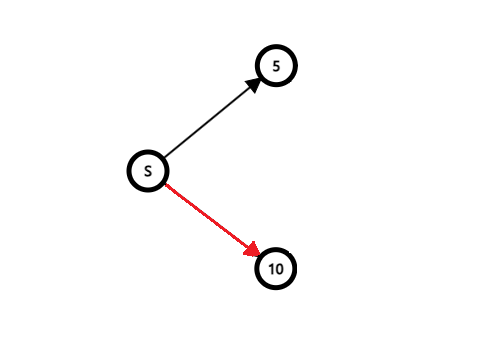
S에서 5 또는 10으로 가는 문제

S에서 5 또는 10으로 가는 문제다. 합을 최대로 만들어야 하므로 현재 상태에서의 최적해는 10이다.

---

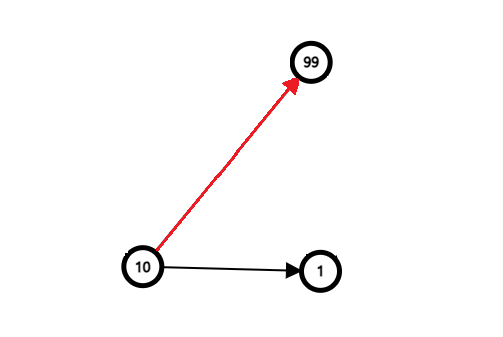
10에서 99 또는 1로 가는 문제

10에서 99로 가는 것이 최적해다.

---

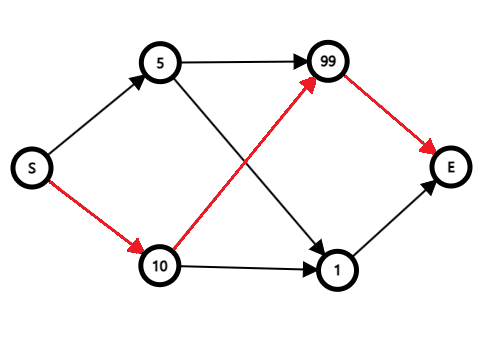
전체 문제의 최적해와 비교

각 부분 문제의 최적해는 10과 99이고, 전체 문제의 최적해와 일치한다. 이런 경우 부분 문제들의 최적해의 집합이 전체 문제의 최적해와 일치한다고 하고 그리디 알고리즘을 사용하여 문제를 풀 수 있다. 이제 일치하지 않는 경우를 보자.

---

부분 문제들의 최적해의 집합이 전체 문제의 최적해와 불일치

위와 동일한 문제를 다른 그래프에 적용했을 때 2가지 부분 문제가 나올 수 있다.

1. S에서 1또는 10으로 가는 문제
2. 1번에서 선택된 노드에서 다음 노드로 가는 문제

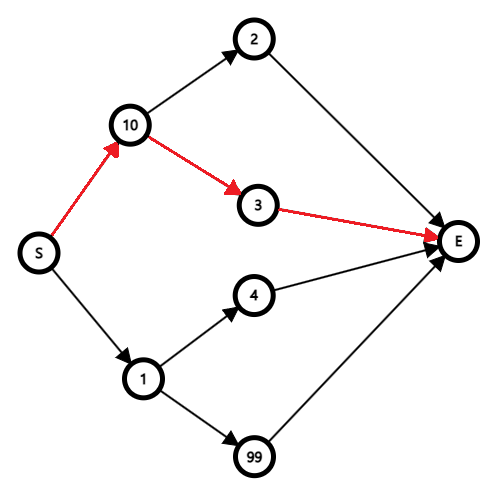
1번 문제의 최적해는 10이고, 2번 문제의 최적해는 3으로 합은 13이다. 전체 문제의 최적해와 비교해보자.

---

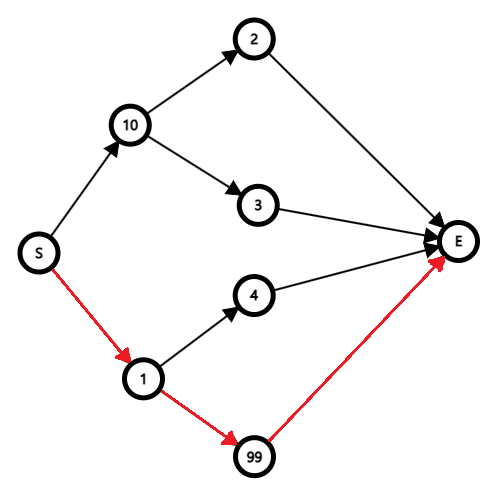
첫 번째 그래프는 부분 문제들의 최적해들의 집합으로, 합은 13이다. 두 번째 그래프는 전체 문제의 최적해로 합은 100이다. 이런 경우 부분 문제들의 최적해의 집합이 전체 문제의 최적해와 불일치한다고 하고 그리디 알고리즘을 사용하여 문제를 풀 수 없다.

---

동전 문제

11047번: 동전 0 문제는 회의실 배정 문제와 더불어 그리디 알고리즘의 대표적인 예제로, N개의 동전의 가치가 주어졌을 때, 동전을 최대한 적게 사용하여 K원을 만드는 문제이다.

---

문제 조건이 위 사진처럼 주어졌다고 가정해보자. 어떤 방식으로 나눠야 동전을 최대한 적게 사용해서 1360원을 만들 수 있을까?

i번째 동전을 추가했을 때, K원을 넘지 않는 동전이 있다면 그 동전들 중 가장 가치가 높은 동전을 사용하는게 항상 최선이다. 답은 위와 같다.

그렇다면 동전 문제는 항상 그리디 알고리즘으로 해결할 수 있을까?

---

새로운 조건의 문제를 동일한 알고리즘으로 풀어보자. 그리디하게 풀 경우 [500, 100, 100, 100]으로 총 4개의 동전을 사용하여 만들 수 있다. 하지만 실제 정답은 [400, 400]으로 2개의 동전만 사용해도 가능하다. 이 문제는 왜 그리디로 풀 수 없을까?

원본 문제에 이런 조건이 있다. “$A_1 = 1, i ≥ 2$인 경우에 $A_i는 A_i-1$의 배수이다”. $i \leq k$인 모든 $A_k$는 $A_i$의 배수이기 때문에, $A_i * q = A_k$라고 가정하면, $q$개의 $A_i$는 항상 1개의 $A_k$로 대체될 수 있다. 따라서 그리디 알고리즘이 성립하는 것이다.

---

코드

#include <bits/stdc++.h>
#define FastIO ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define pb push_back
using namespace std;

int N, K, ans;
vector<int> v;


void Output() {
    cout << ans;
}


void Solve() {
    for(int i = v.size() - 1; i >= 0; i--) {
        ans += (K / v[i]);
        K %= v[i];
    }
}


void Input() {
    cin >> N >> K;
    
    for(int i = 0; i < N; i++) {
        int num;
        cin >> num;
        
        v.pb(num);
    }
}


int main() {
    FastIO;
    
    Input();
    Solve();
    Output();
}

---

기타

그리디 알고리즘 분석하기