웰노운 테크닉(추가 예정)

웰노운 테크닉

웰노운(진짜 웰노운)이지만, 따로 작성하기엔 양이 적은 테크닉들 모음.

---

상하좌우 탐색

(x, y)를 기준으로 상하좌우 좌표를 생각해보자. x의 변화량은 {-1, 1, 0, 0}이고, y의 변화량은 {0, 0, -1, 1}이다. 이것을 dx, dy배열로 만들어서 상하좌우 좌표를 계산하는 테크닉이다. 2차원의 4방향뿐만 아니라, N차원의 M방향은 전부 표현 가능하다.

코드

int dx[4] = {-1, 1, 0, 0};
int dy[4] = {0, 0, -1, 1};
bool visited[r][c];

void search(int x, int y) {
    for(int i = 0; i < 4; i++) {
        int nx = x + dx[i];
        int ny = y + dy[i];

        if(nx < 0 || nx >= r || ny < 0 || ny >= c || visited[nx][ny]) {
            continue;
        }

        visited[nx][ny] = true;
    }
}

---

벽 유무 판별

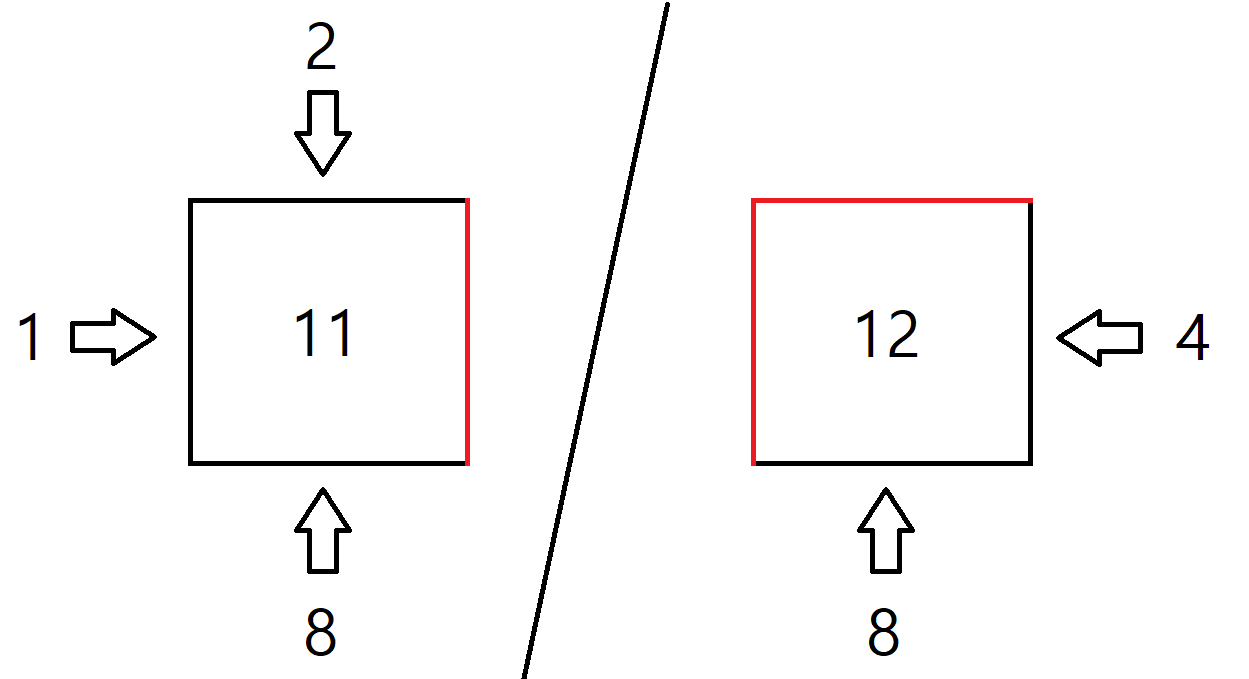(일반적으로) 2차원 평면에서 상하좌우로 이동하려고 할 때, 벽의 존재여부를 판별하는 방법이다. 벽에 좌상우하 순서대로 각각 {1, 2, 4, 8}을 부여한다. 그리고 각 칸의 값은 칸에 존재하는 벽의 값의 합이다. 예를 들어서 4방향 전부 벽이 있다면 15, 하나도 없다면 0, 우하에 벽이 있다면 12가 칸의 값이다.

이제 비트마스킹을 통해 각 벽의 존재여부를 판별할 수 있다. 칸의 값과 각 벽의 값을 & 연산을 했을 때, 결과가 벽의 값과 같다면 벽이 존재하고, 0이면 벽이 존재하지 않는다.

벽에 부여하는 숫자의 값이나 순서는 임의대로 설정해도 상관없다.

코드

int r, c;
int board[50][50];
int wall_bit[4] = {1, 2, 4, 8};

void CheckWall() {
    for(int x = 0; x < r; x++) {
        for(int y = 0; y < c; y++) {
            for(int i = 0; i < 4; i++) {
                if((board[x][y] & wall_bit[i]) == wall_bit[i]) {
                    // exist wall
                }
            }
        }
    }
}

---

순열

int n, r; // init
int arr[n] // init
bool visited[n]; 

void nPr(int depth) {
    if(depth == r) {
        for(int i = 0; i < n; i++) {
            if(visited[i]) {
                cout << i << " ";
            }
        }
        cout << '\n';
    }

    for(int i = 0; i < n; i++) {
        if(visited[i]) {
            continue;
        }

        visited[i] = true;
        nPr(depth + 1);
        visited[i] = false;
    }
}

---

조합

int n, r; // init
int arr[n]; // init
bool visited[n]; 

void nCr(int depth, int last) {
    if(depth == r) {
        for(int i = 0; i < n; i++) {
            if(visited[i]) {
                cout << i << " ";
            }
        }
        cout << '\n';
    }

    for(int i = last; i < n; i++) {
        if(visited[i]) {
            continue;
        }

        visited[i] = true;
        nCr(depth + 1, i + 1);
        visited[i] = false;
    }
}

---

트리의 지름

트리의 지름