큐
큐
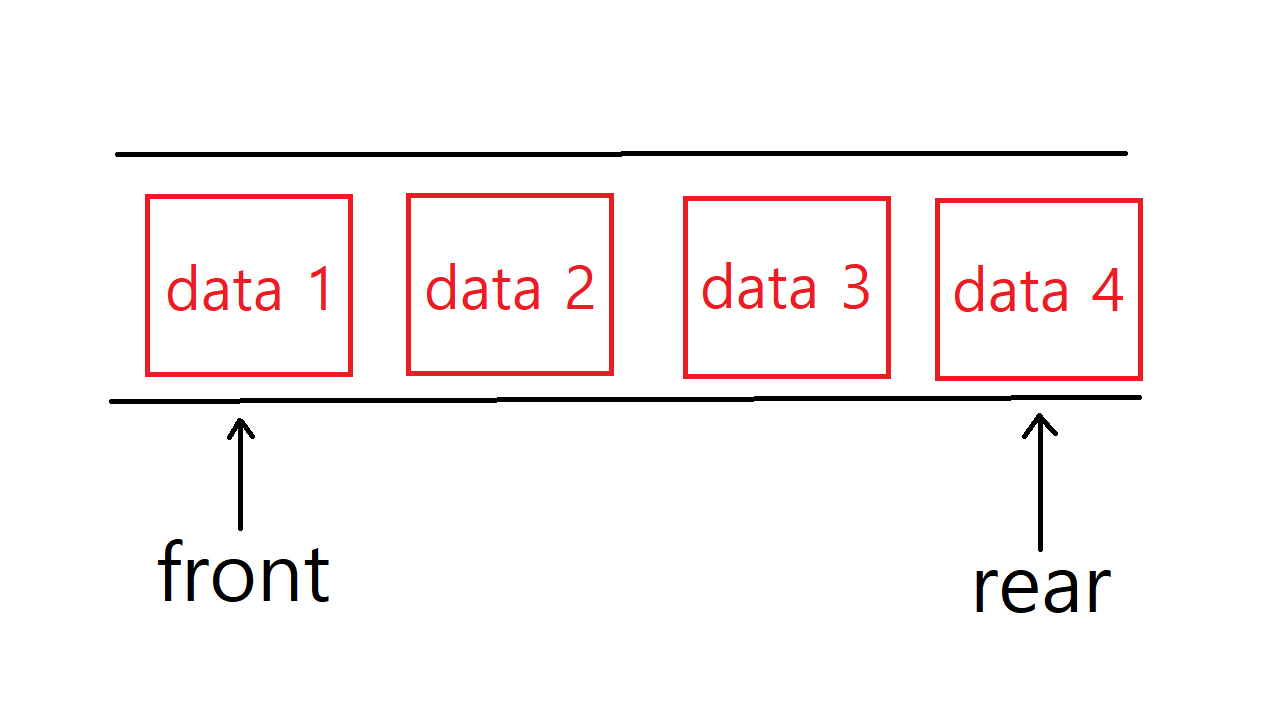
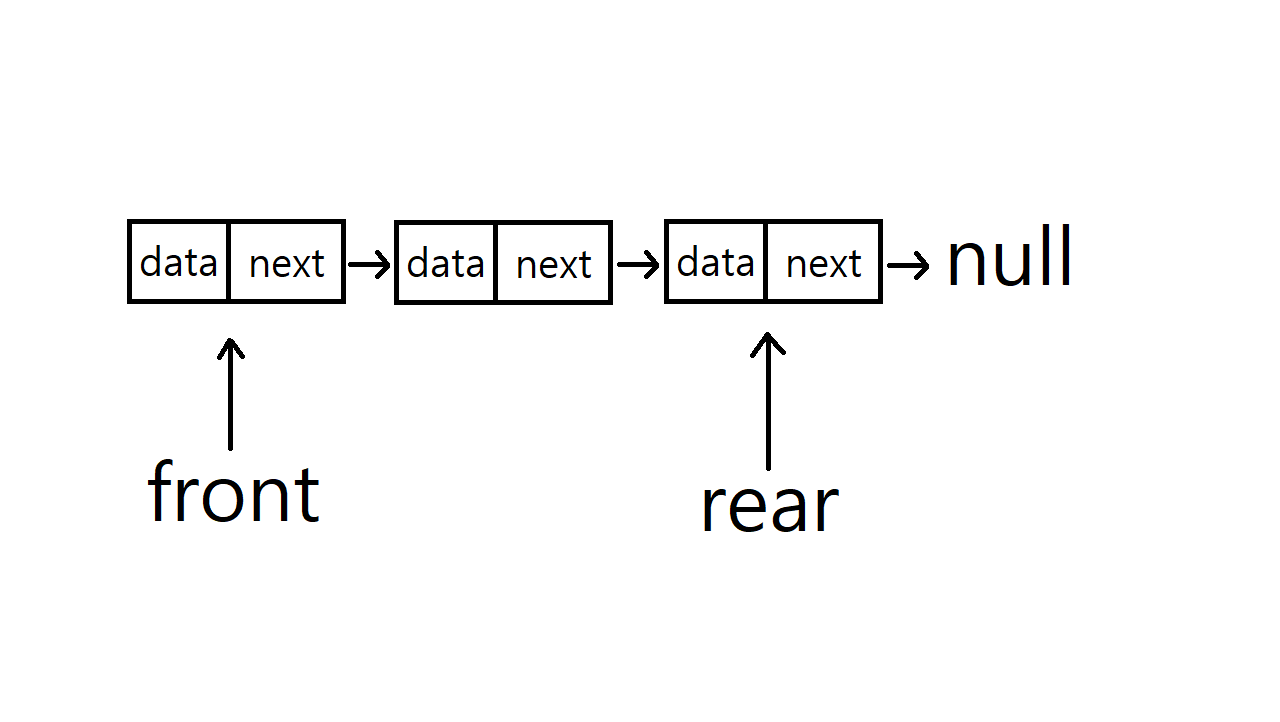
큐는 먼저 추가된 데이터가 먼저 삭제되는 선입선출(FIFO: First Input FIrst Out)구조를 가지고 있는 자료구조이다. 큐의 종류에는 선형 큐와 원형 큐가 있다. 큐에서 삭제가 일어나는, 즉 가장 앞에 있는 곳을 front, 삽입이 일어나는 가장 뒤에 있는 곳을 rear이라고 한다.
큐 ADT
| element E |
| add(E e) | 큐의 맨 앞에 데이터를 추가한다. |
| poll() | 큐의 맨 앞의 데이터를 제거하고 반환한다. |
| peek() | 큐의 맨 앞의 데이터를 반환한다. |
| size() | 큐의 크기를 반환한다. |
| isEmpty() | 큐가 비어있는지 검사한다. |
큐의 삽입 연산
큐의 가장 뒤에 데이터를 추가한다.
큐의 삭제 연산
큐의 가장 앞에 있는 데이터를 삭제한다.
선형 큐
배열, 연결리스트를 사용해 구현했을 때의 장단점은 스택과 동일하다.
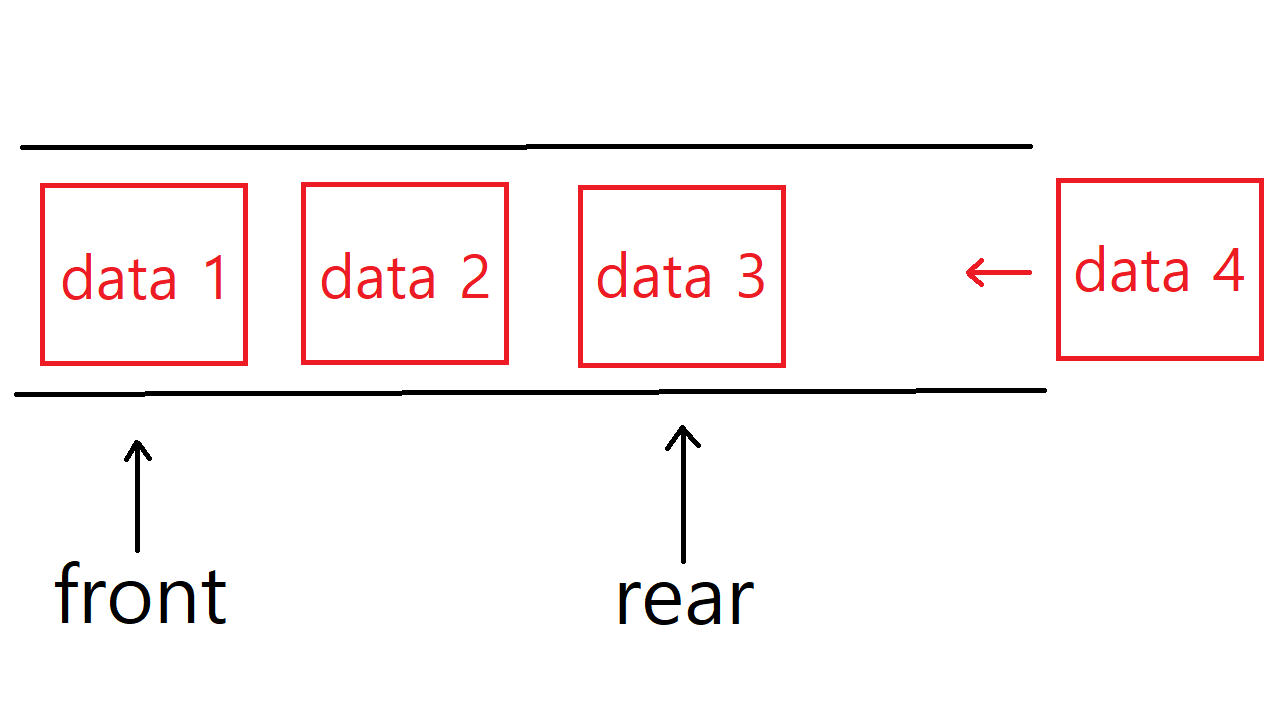
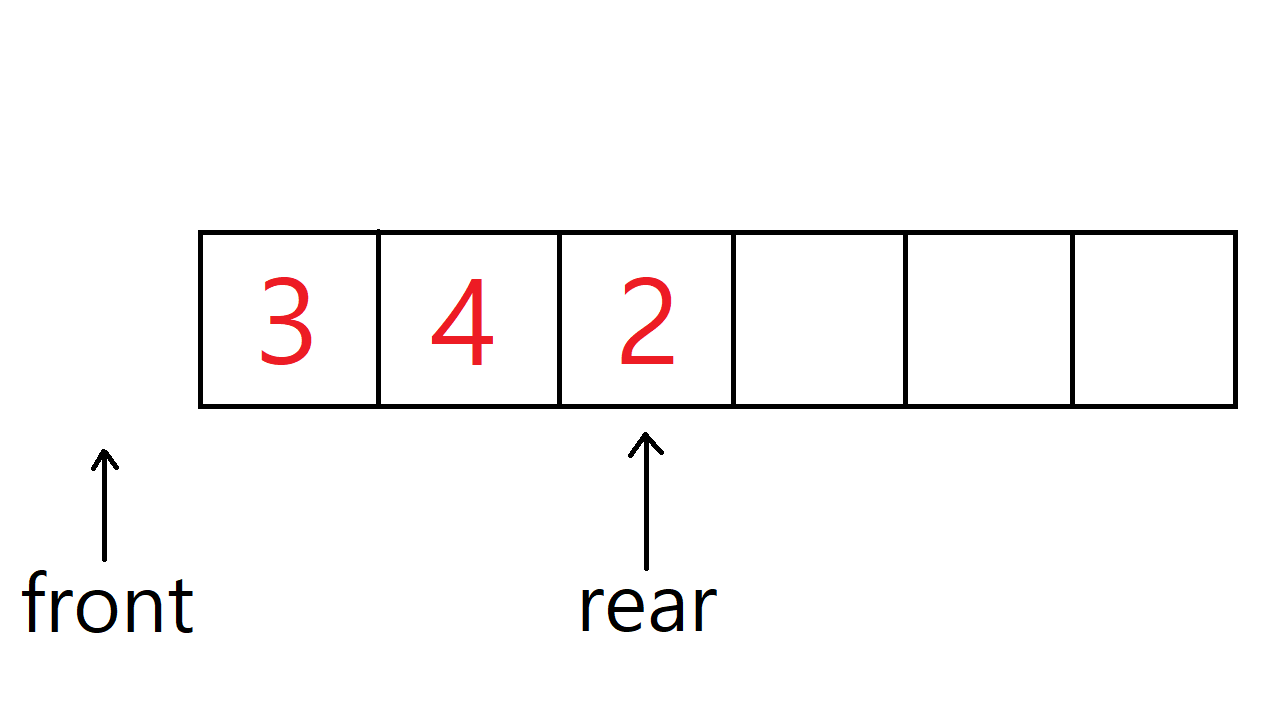
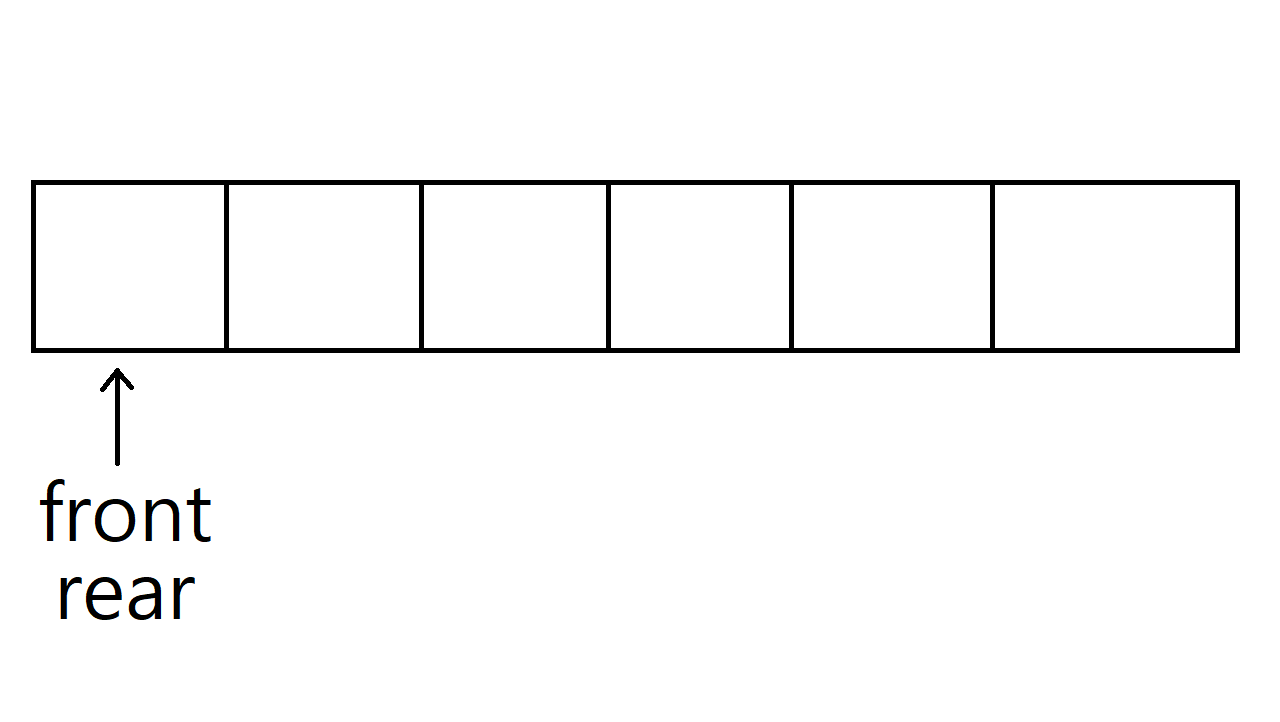
배열을 이용한 선형 큐의 삽입 연산
실제로 배열을 사용해서 큐를 구현할 때는 rear는 가장 마지막에 추가된 데이터, front는 가장 처음에 추가된 데이터보다 한 칸 앞을 가리키고 있다. 초기값은 둘 다 -1이며, front와 rear의 값이 같다면 큐가 비어있다는 의미다. 데이터를 추가할때마다 rear 값을 1씩 더해주면 된다.
정수 3, 4, 2를 순서대로 추가했을 때 큐의 모양이다. rear는 가장 마지막에 추가된 2를, front는 가장 처음에 추가된 데이터인 3의 index가 0이므로 -1을 가리키고 있다.
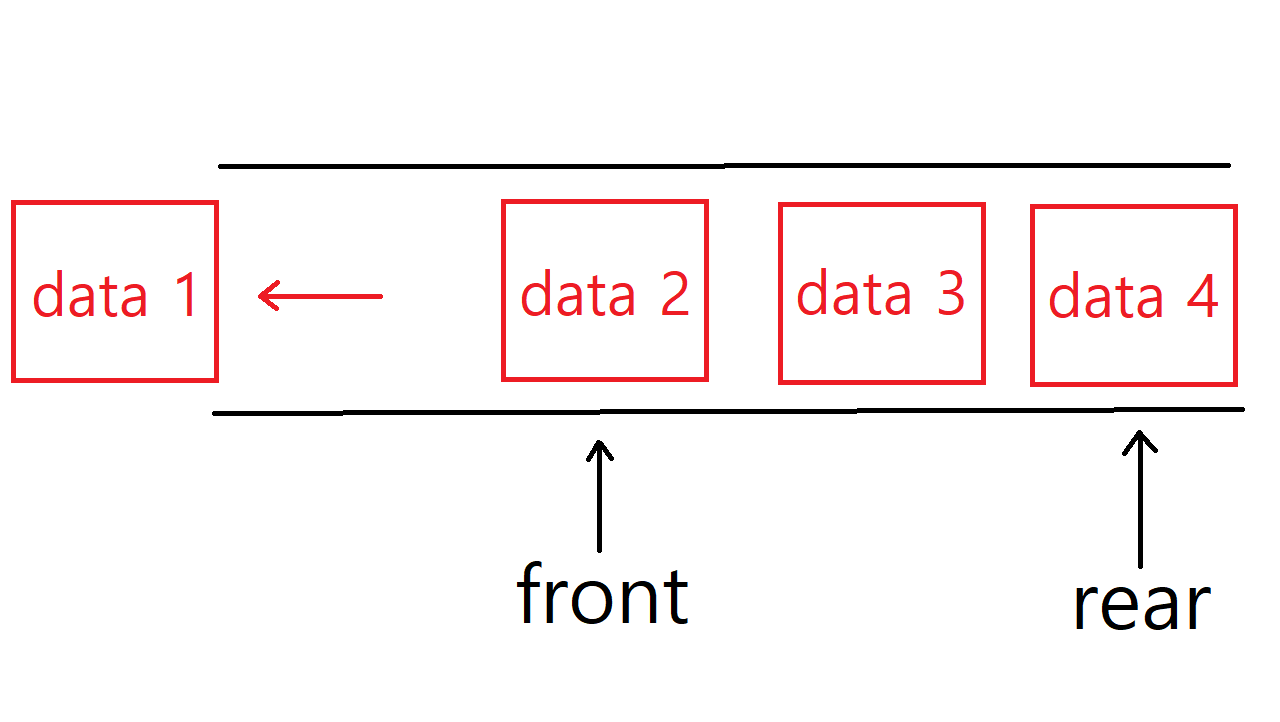
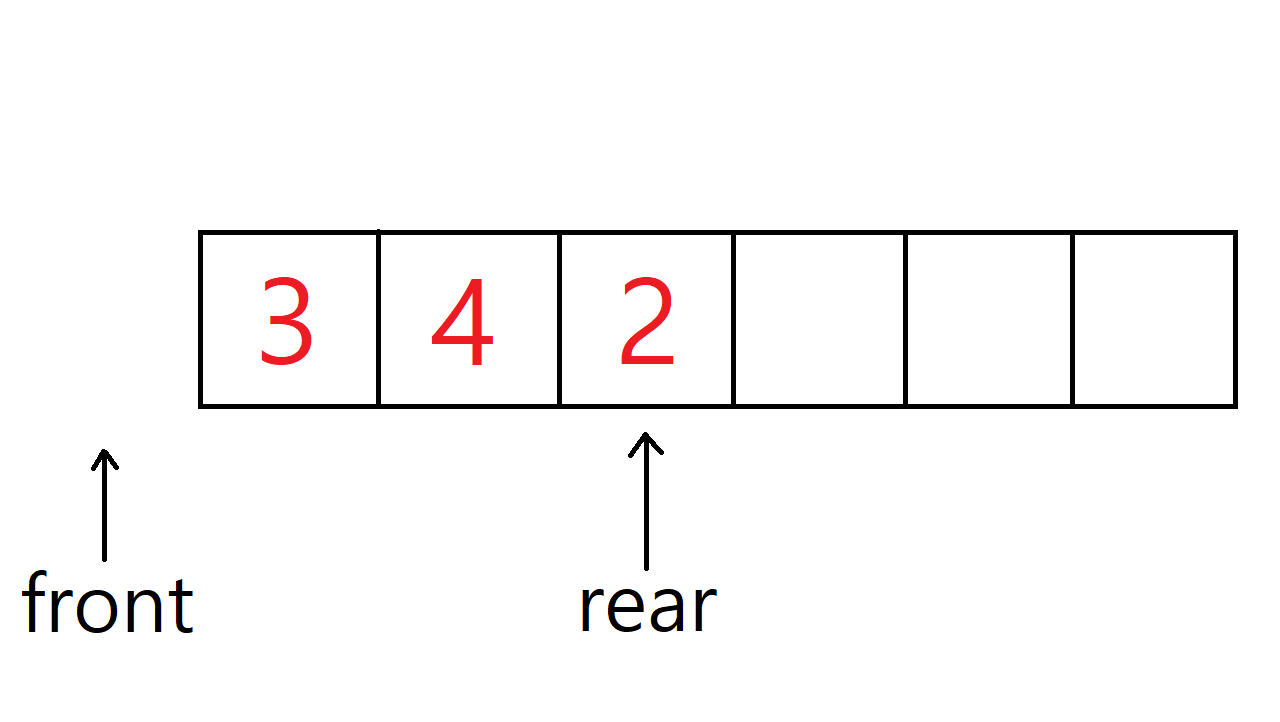
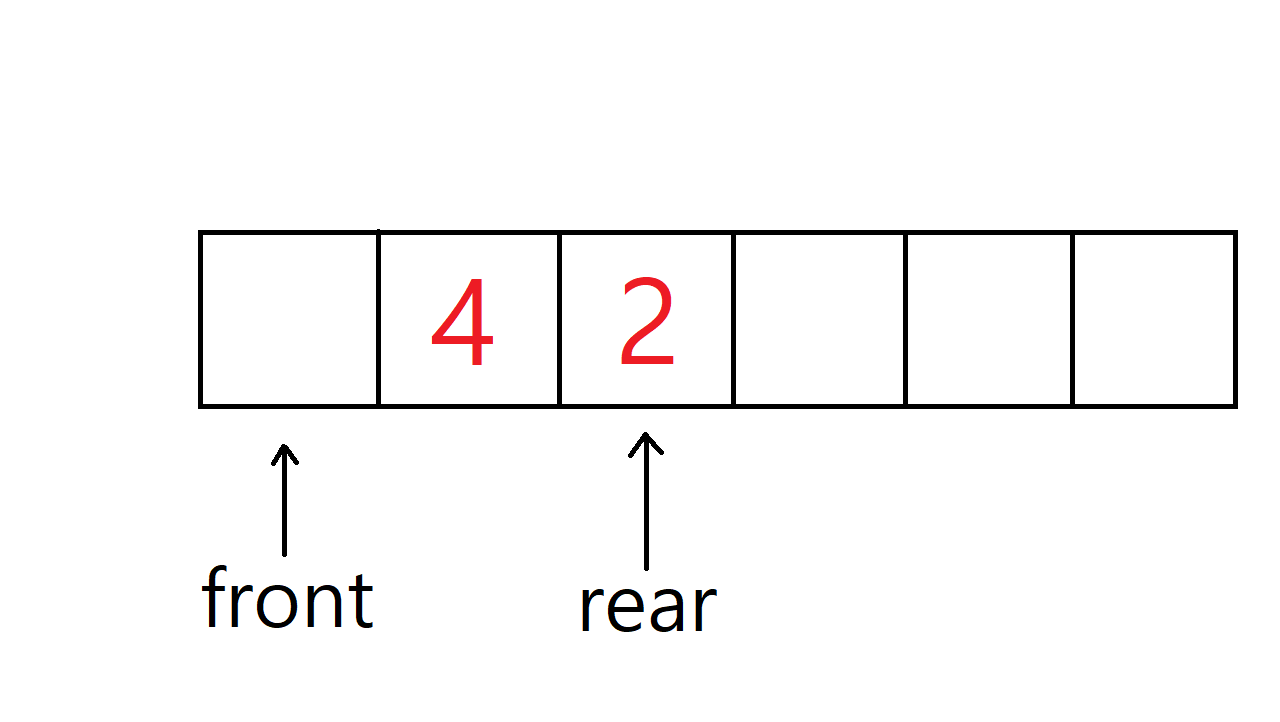
배열을 이용한 선형 큐의 삭제 연산
정수 3, 4, 2가 저장된 큐에서 3을 삭제한 후 큐의 모습이다. 데이터가 삭제될때마다 front 값을 1씩 더해주면 된다.
배열을 이용한 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Queue<E> {
private E[] data;
private int capacity;
private int front;
private int rear;
Queue() {
capacity = 100;
front = rear = -1;
data = (E[]) new Object[capacity];
}
private void grow() {
capacity += 100;
E[] newData = Arrays.copyOfRange(data, 0, capacity);
data = newData;
}
public void add(E e) {
if(rear == capacity - 1) {
grow();
}
data[++rear] = e;
}
public E poll() {
if(isEmpty()) {
throw new ArrayIndexOutOfBoundsException();
}
else {
return data[++front];
}
}
public E peek() {
if(isEmpty()) {
throw new ArrayIndexOutOfBoundsException();
}
else {
return data[rear];
}
}
public int size() {
return rear - front;
}
public boolean isEmpty() {
if(front == rear) {
return true;
}
else {
return false;
}
}
}
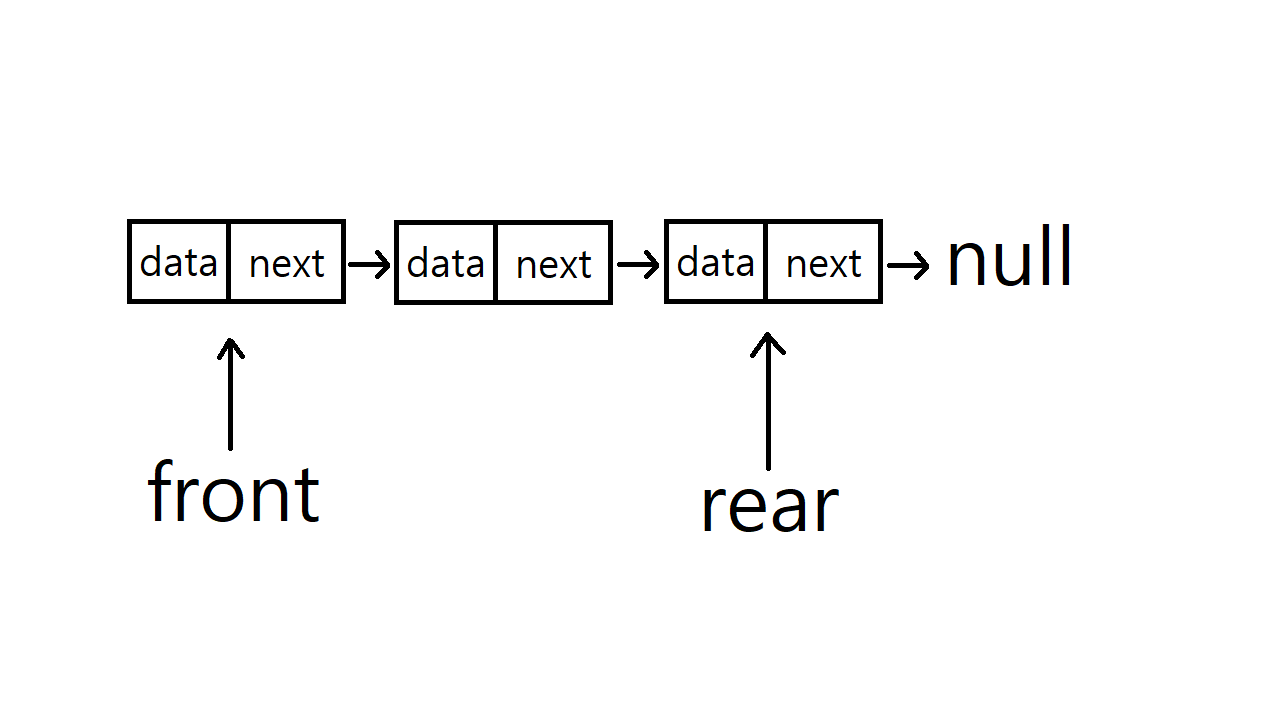
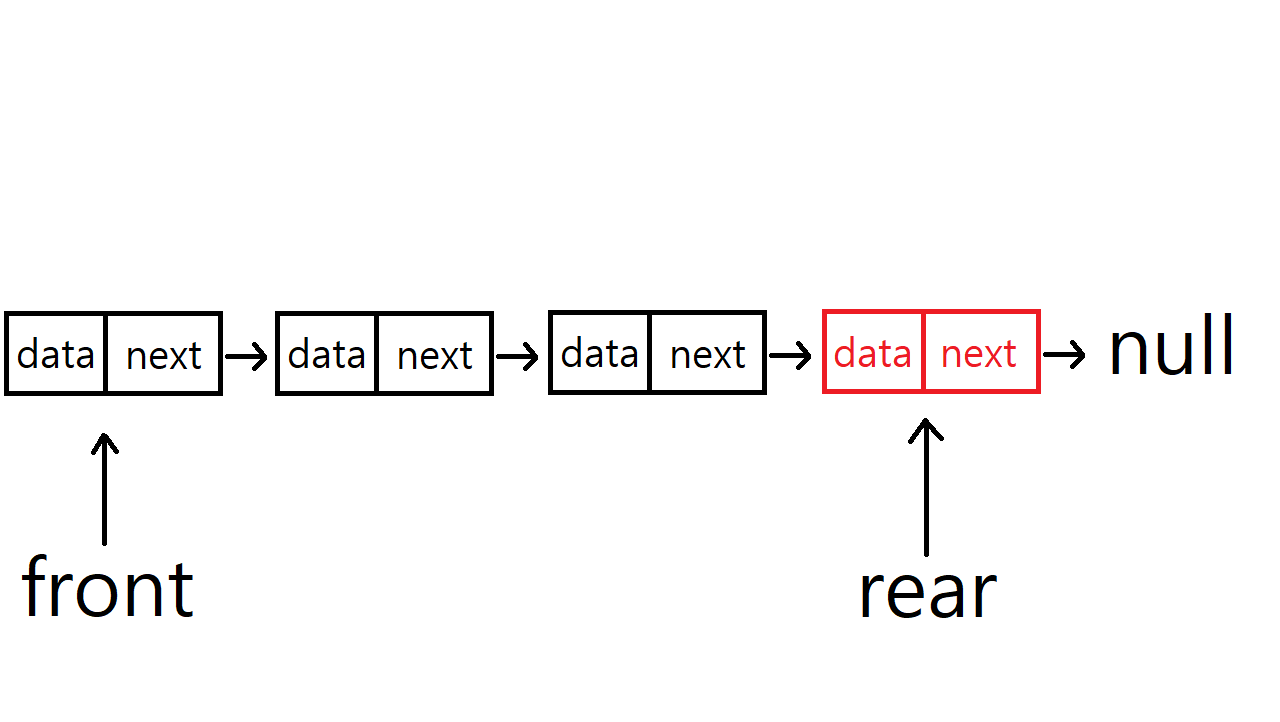
연결 리스트를 이용한 선형 큐의 삽입 연산
연결 리스트로 큐를 구현했을 때 front는 가장 처음에 추가된 노드를, rear는 가장 마지막에 추가된 노드를 가리키고 있다. 초기값은 front, rear 둘 다 null이다.
삽입 연산은 단순 연결 리스트에서의 삽입 연산과 동일하다.
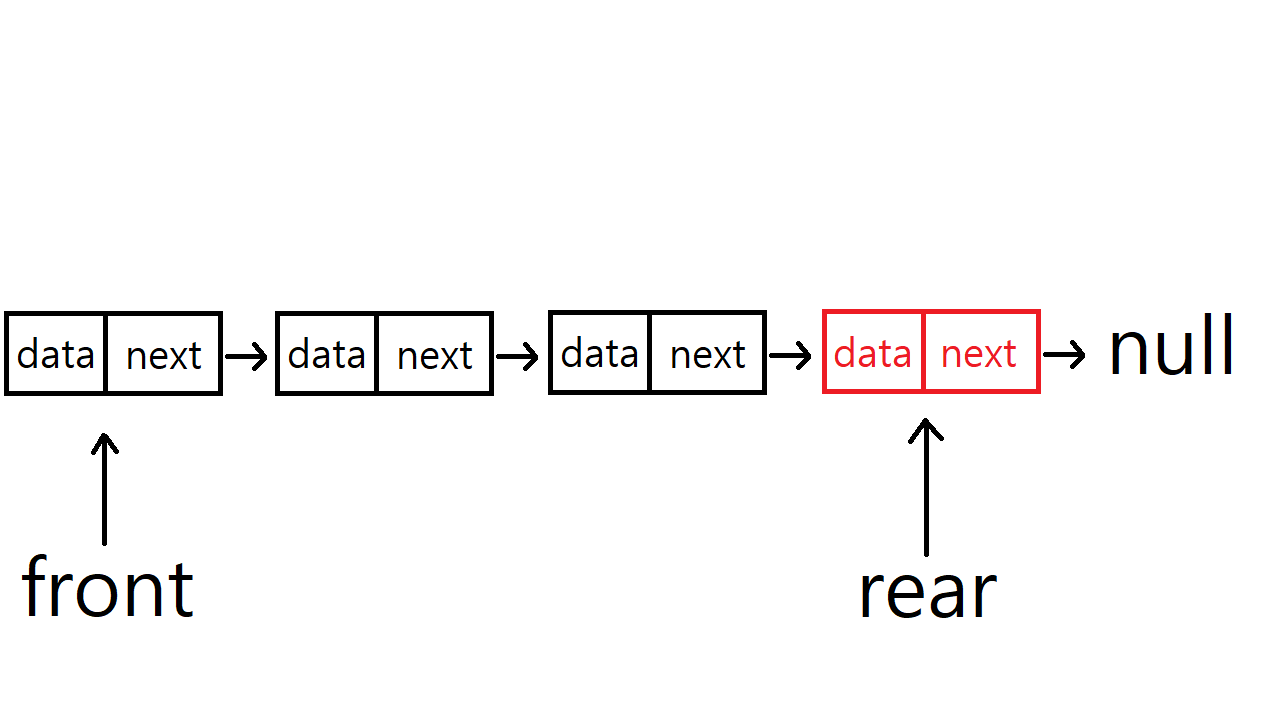
연결 리스트를 이용한 선형 큐의 삭제 연산
삭제 연산도 단순 연결 리스트에서의 remove(0) 연산과 동일하다.
연결 리스트를 이용한 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
class Queue<E> {
private Node<E> front = null;
private Node<E> rear = null;
private int queueSize = 0;
private class Node<E> {
E data;
Node<E> next;
Node(E data) {
this.data = data;
this.next = null;
}
}
public void add(E e) {
Node<E> node = new Node(e);
if(isEmpty()) {
front = rear = node;
}
else {
rear.next = node;
rear = node;
}
queueSize++;
}
public E poll() {
if(isEmpty()) {
throw new NullPointerException();
}
else {
E ret = front.data;
front = front.next;
queueSize--;
if(queueSize == 0) {
rear = null;
}
return ret;
}
}
public E peek() {
if(isEmpty()) {
throw new NullPointerException();
}
else {
return front.data;
}
}
public int size() {
return queueSize;
}
public boolean isEmpty() {
if(front == null && rear == null) {
return true;
}
else {
return false;
}
}
}
원형 큐
선형 큐를 배열로 구현했을 때 치명적인 단점이 있다. 스택은 배열로 구현하더라도 top이 증가 혹은 감소하기 때문에 할당한 메모리를 전부 사용할 수 있지만, 큐의 front와 rear는 단조 증가하기 때문에 할당한 메모리를 전부 사용할 수 없다. 배열로 구현한 큐가 꽉 찰 때까지 add() 연산을 한 후, 큐가 빌 때까지 remove() 연산을 한다고 생각해보자. 큐가 비어있음에도 front와 rear 전부 큐의 마지막 index를 가리키고 있다. 이런 문제를 해결하기 위해 원형 큐 구조를 사용한다.
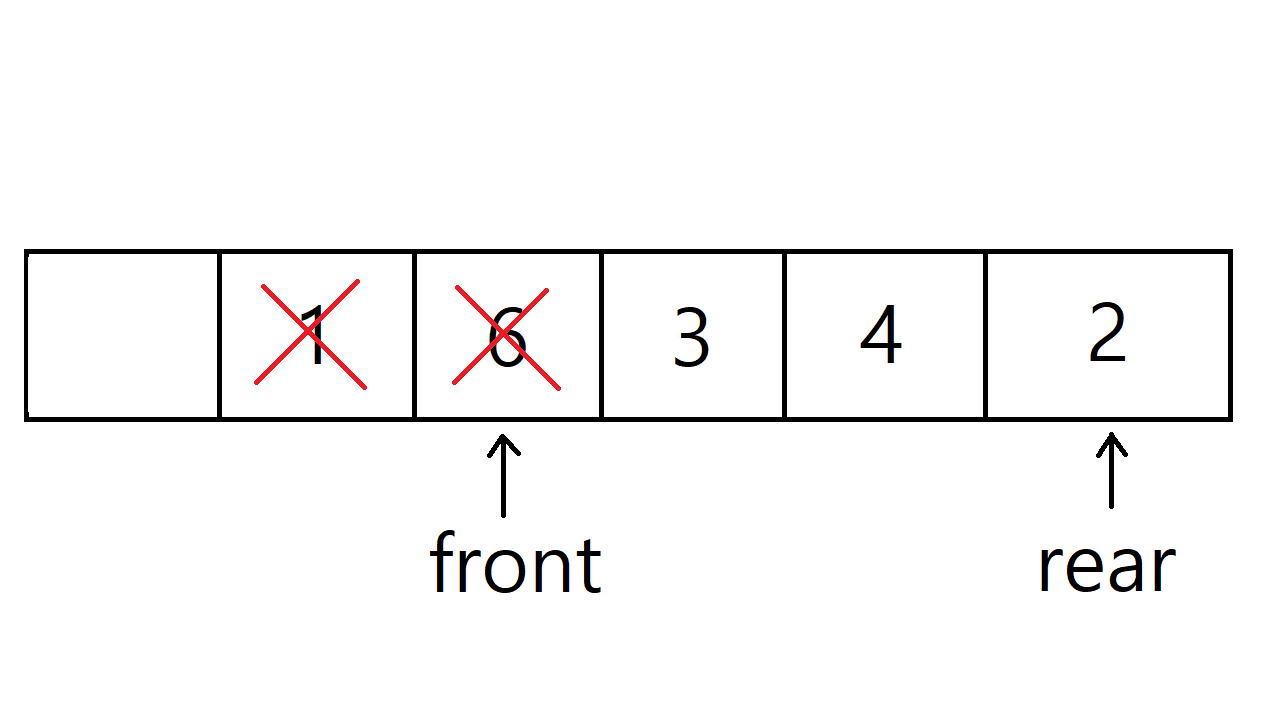
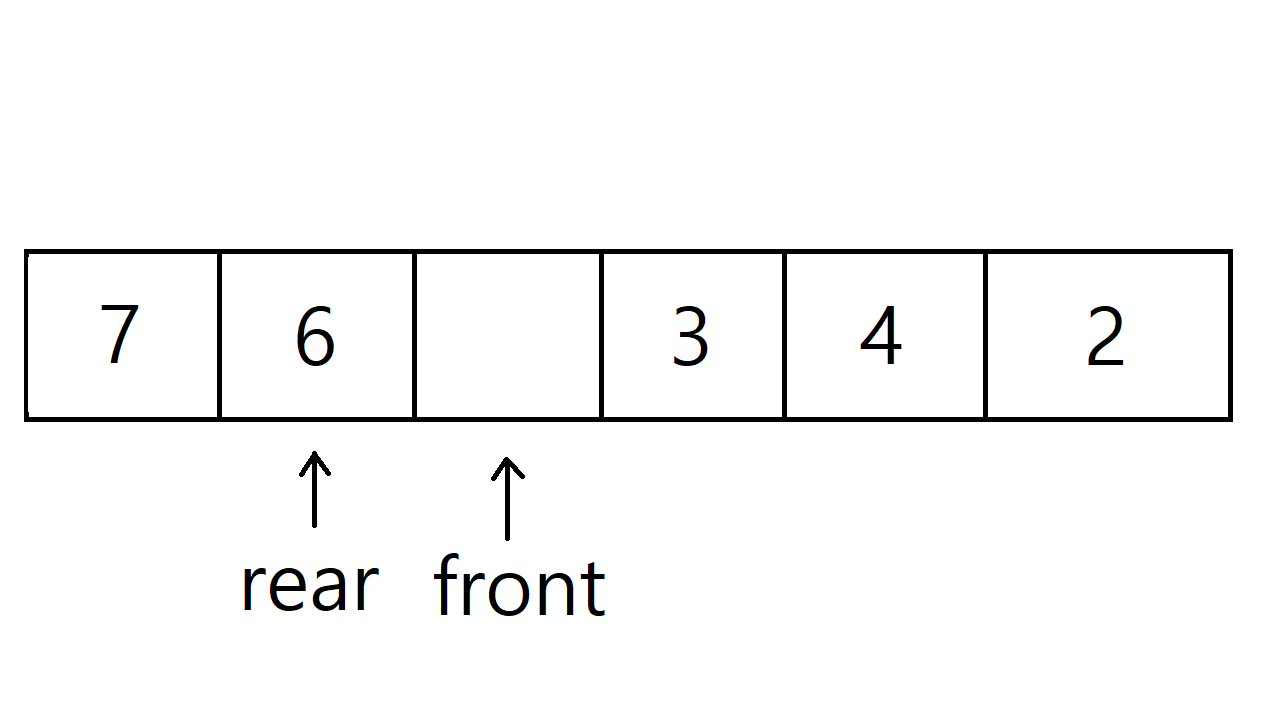
원형 큐도 기본적인 구조는 선형 큐와 동일하다. 차이점이라면 front, rear의 초기값이 -1이었던 선형 큐와 달리 원형 큐는 초기값이 0이다.
위의 큐는 정수 1, 6, 3, 4, 2를 추가한 후 1, 6을 제거한 후의 원형 큐다. 선형 큐라면 위와 같은 상황에서 더 이상 정수를 추가할 수 없겠지만 원형 큐는 가능하다. 선형 큐는 원소를 추가할 때 rear 값에 단순히 1을 더했지만, 원형 큐는 rear = (rear + 1) % capacity 연산을 한다. 모듈러 연산을 통해 index를 원형으로 이용한다는 뜻이다. 위의 큐에서 원소를 추가하려고 할 때의 rear 값은 (5 + 1) % 6이다. 즉, index 0에 원소를 추가할 수 있다.
원형 큐에서도 신경써야 할 부분이 하나 있는데, 포화 상태와 공백 상태를 구분하기 위해서 한 칸은 공백을 유지해야 한다는 것이다. 원형 큐에서도 선형 큐와 동일하게 front와 rear의 값이 같을 때 공백 상태이다. 그렇기 때문에 한 칸을 공백으로 유지하지 않을 경우, rear와 front가 같을 때 다른 변수 없이는 공백 상태인지 포화 상태인지 판단할 수 없다.
원형 큐 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
class Queue<E> {
private E[] data;
private int capacity;
private int front;
private int rear;
private int queueSize;
Queue() {
queueSize = 0;
capacity = 100;
front = rear = 0;
data = (E[]) new Object[capacity];
}
private void grow() {
E[] newData = (E[]) new Object[capacity + 100];
for(int i = 1; i <= queueSize; i++) {
newData[i] = data[(front + i) % capacity];
}
capacity += 100;
front = 0;
rear = queueSize;
data = newData;
}
public void add(E e) {
if((rear + 1) % capacity == front) {
grow();
}
rear = (rear + 1) % capacity;
data[rear] = e;
queueSize++;
}
public E poll() {
if(isEmpty()) {
throw new ArrayIndexOutOfBoundsException();
}
else {
front = (front + 1) % capacity;
queueSize--;
return data[front];
}
}
public E peek() {
if(isEmpty()) {
throw new ArrayIndexOutOfBoundsException();
}
else {
return data[(front + 1) % capacity];
}
}
public int size() {
return queueSize;
}
public boolean isEmpty() {
if(front == rear) {
return true;
}
else {
return false;
}
}
}
컬렉션 프레임워크
Queue
Queue는 리스트, 스택과 다르게 클래스가 아니라 인터페이스다. 객체를 직접 만들 수 없는 인터페이스 특성상 Queue