레드-블랙 트리(추가 예정)
레드-블랙 트리
레드-블랙 트리는 높이를 $Klog_2(N)$으로 유지하는 자가 균형 이진 트리이다. 모든 노드가 red 혹은 black 색깔을 가지고 있으며, 다른 트리들과 다르게 NIL(NULL)노드를 표시한다.
레드-블랙 트리의 성질
- 모든 노드는 red or black node이다.
- 루트 노드는 항상 black node이다.
- 리프 노드는 항상 black node이다.
- red node의 자식은 항상 black node이다.
- 임의의 노드에서 리프 노드로 가는 경로에서 거치는 black node의 개수는 항상 같다.
레드-블랙 트리의 높이 증명
5번 성질을 바탕으로 레드-블랙 트리의 높이가 항상 $Klog_2(N)$을 유지한다는 것을 증명해보자. 그러기 위해서는 두 가지 용어의 정의와, 두 가지 명제의 증명이 필요하다.
용어 정의 h(n) = 노드 n을 루트 노드로 하는 서브 트리의 높이 bh(n) = 노드 n에서 리프 노드까지 가는 경로에서 만나는 노드 n을 제외한 black node의 개수.
명제
- n의 서브 트리의 내부 노드의 개수 $\ge 2^{bh(n)} - 1$
- bh(root) $\ge$ $h/2$
1번 명제
1번 명제는 h(n)에 대한 귀납법으로 증명할 것이다.
- h(n) = 0에서 성립하는가?
- h(n) $\le$ k에서 성립한다고 가정했을 때, h(n) $\le$ k + 1에서 성립하는가?
h(n) = 0에서 성립하는가?
높이가 0인 트리를 생각해보자. 그 트리는 null 노드만 존재하는 트리일 것이다. null노드의 서브 트리의 내부 노드의 개수는 0개이고 bh(n)도 0이므로 h(n) = 0에서 명제가 성립함을 알 수 있다.
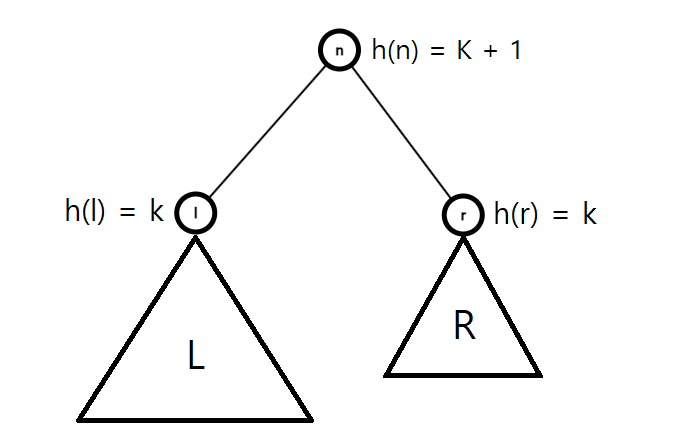
h(n) ≤ k에서 성립한다고 가정했을 때, h(n) ≤ k + 1에서 성립하는가?
위 트리에서 bh(l), bh(r)값에 대해 생각해보자. bh(l)과 bh(r)이 가질 수 있는 값은 bh(n) 혹은 bh(n) - 1이다. 만약 l이 red node라면 bh(l) = bh(n)일 것이고, black node라면 bh(l) = bh(n) - 1일 것이다. 이는 l을 r로 바꿔도 유효하다. 따라서 bh(l), bh(r) $\ge$ bh(n) - 1이 성립한다.
다음으로 l, r의 서브 트리인 L, R의 내부 노드의 개수에 대해 생각해보자. 1번 명제가 임의의 노드 v에 대해 h(v) $\le$ k면 성립한다고 가정했으므로 l, r에서도 성립한다고 가정한다. 따라서 L의 내부 노드의 개수 $\ge 2^{bh(l)} - 1$, R의 내부 노드의 개수 $\ge 2^{bh(r)} - 1$이 성립한다.
마지막으로 n의 서브 트리의 내부 노드의 개수에 대해 생각해보자. n의 서브 트리의 내부 노드의 개수는 L의 내부 노드의 개수 + R의 내부 노드의 개수 + 1(자기 자신)이다. L의 내부 노드의 개수 + R의 내부 노드의 개수는 $2^{bh(l)} - 1 + 2^{bh(r)} - 1$로 치환할 수 있고, bh(l), bh(r)을 bh(n) - 1로 치환하면 $2^{bh(n) - 1} - 1 + 2^{bh(n) - 1} - 1$이 된다.
이제 식을 정리해보자.
n의 서브 트리의 내부 노드의 개수 $\ge 2^{bh(n) - 1} - 1 + 2^{bh(n) - 1} - 1 + 1$
n의 서브 트리의 내부 노드의 개수 $\ge 2 * 2^{bh(n) - 1} - 1$
n의서브 트리의 내부 노드의 개수 $\ge 2^{bh(n)} - 1$
이렇게 1번 명제를 증명할 수 있다.
2번 명제
2번 명제는 간단하다. h(root) = 0일 때, bh(root) = 0, h/2 = 0이므로 bh(root) $\ge$ $h/2$가 성립한다. 이 트리에 자식 노드가 추가된다고 생각해보자. 추가된 자식 노드가 black node일 경우 좌변은 1, 우변은 1/2씩 증가하므로 여전히 성립한다. red node가 추가될 경우에도 red node는 항상 자식 black node(null node)를 동반하므로 이 경우에도 명제가 성립함을 알 수 있다.
높이 유지 증명
이제 1, 2번 명제를 토대로 레드-블랙 트리의 높이가 항상 $Klog_2(N)$이라는 것을 증명할 것이다. 우선 레드-블랙 트리의 루트 노드를 root, 전체 노드의 개수를 n이라고 정의하자.
root의 서브 트리의 내부 노드의 개수는 트리의 전체 노드 개수와 같다.
따라서 1번 명제에 의해 트리의 전체 노드의 개수 $\ge 2^{bh(root)} - 1$가 성립한다. 또한 2번 명제에 의해 트리의 전체 노드의 개수 $\ge 2^{h/2} - 1$로 치환할 수 있다.
$n \ge 2^{h/2} - 1$을 정리해보자.
$n + 1 \ge 2^{h/2}$
$log_2(n + 1) \ge h/2$
$h \le 2 * log_2(n + 1)$
따라서 레드-블랙 트리의 높이 h는 $h \le 2 * log_2(n + 1)$ 상태로 유지됨을 알 수 있다.