분리 집합(Disjoint Set)
분리 집합
분리 집합은 공통 원소가 없는 집합(서로소 집합)들에 대한 정보를 저장하고 조작하는 자료 구조이다. 두 원소가 같은 집합에 속해있는지 확인하거나, 최소 신장 트리를 구현하는 등 여러 상황에서 사용할 수 있다.
분리 집합은 유니온 파인드라고도 하는데, 분리 집합이 Union과 Find 두 가지 연산을 지원하기 때문이다.
연산
Union
Union은 두 개의 집합을 하나의 집합으로 합치는 연산이다. Union(a, b)가 집합 a와 집합 b를 합치는 연산이라고 정의하자.
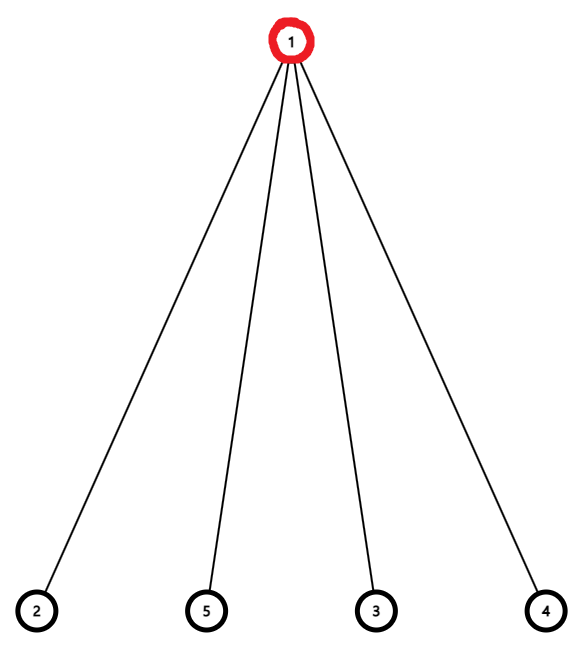
처음에는 {1}, {2}, {3}, {4}, {5}, {6} 총 6개의 집합이 존재한다.
위의 상태에서 Union({1}, {2})와 Union({3}, {4})를 수행한 결과이다. 이제 {1, 2}, {3, 4}, {5}, {6} 총 4개의 집합이 존재한다.
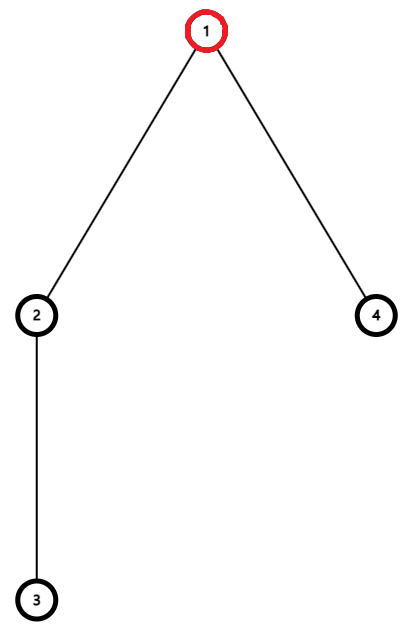
Union을 수행한 집합에 다시 Union을 수행할 수도 있다. Union({1, 2}, {3, 4})를 수행한 결과이다. {1, 2, 3, 4}와 {5}, {6} 총 3개의 집합이 존재한다.
Find
Find는 해당 원소가 포함되어 있는 집합을 찾는 연산이다. 일반적으로 해당 원소가 속한 집합을 대표하는 원소를 반환한다. Find(a)를 원소 a가 포함된 집합을 찾는 연산이라고 정의하자.
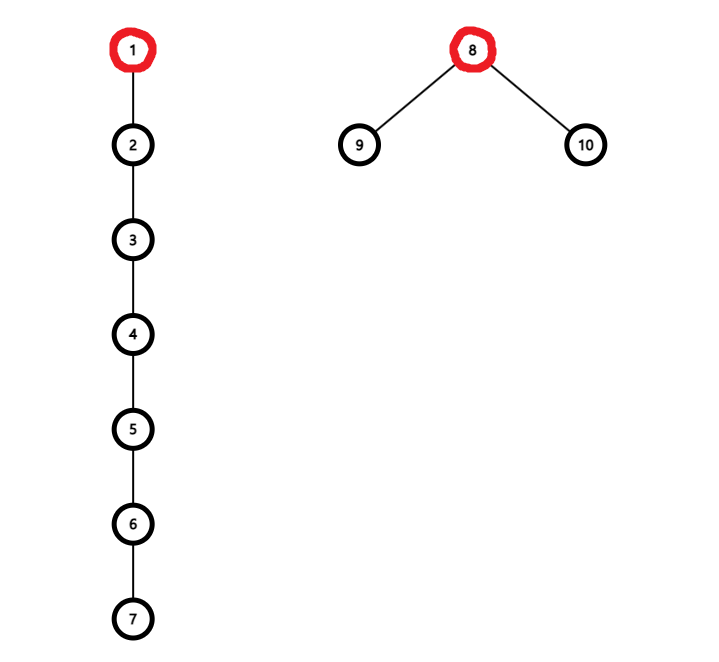
집합 {1, 2, 3, 4}를 1번이 루트 노드인 트리 형태로 표현한 것이다. 따라서 집합의 대표 원소도 1번이 된다. 대표 원소는 해당 집합의 원소 중에서 아무거나 선택하면 된다. Find(1), Find(2), Find(3), Find(4) 모두 1을 반환한다.
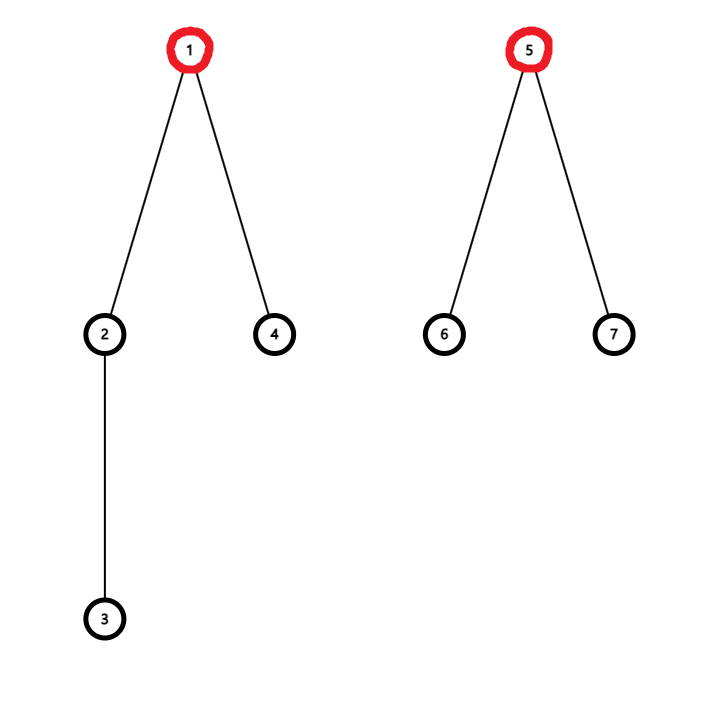
집합 {1, 2, 3, 4}와 {5, 6, 7}을 트리 형태로 표현한 것이다. 루트 노드는 각각 1번과 5번이다.
Find(1), Find(2), Find(3), Find(4) 모두 1을 반환하고, Find(5), Find(6), Find(7)은 모두 5를 반환한다. 이처럼 Find를 통해 임의의 두 원소가 같은 집합에 속하는지 알 수 있다.
구현
1717번: 집합의 표현의 코드이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <bits/stdc++.h>
#define FastIO ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define ll long long
using namespace std;
int n, m;
int parent[1000001];
int Find(int cur) {
if(parent[cur] == cur) {
return cur;
}
return Find(parent[cur]);
}
void Union(int a, int b) {
a = Find(a);
b = Find(b);
if(a == b) {
return;
}
parent[a] = b;
}
void Query() {
int q, a, b;
for(int i = 0; i < m; i++) {
cin >> q >> a >> b;
if(q == 0) {
Union(a, b);
}
else {
if(Find(a) == Find(b)) {
cout << "YES" << '\n';
}
else {
cout << "NO" << '\n';
}
}
}
}
void Init() {
for(int i = 0; i <= n; i++) {
parent[i] = i;
}
}
void Solve() {
Init();
Query();
}
void Input() {
cin >> n >> m;
}
int main() {
FastIO;
Input();
Solve();
}
구현 최적화
위의 코드를 제출하면 TLE를 받는다. Union과 Find의 시간 복잡도를 계산해보자.
Union의 시간 복잡도는 Union 내부의 Find를 제외하면 $O(1)$이므로 Find의 시간 복잡도에 비례한다.
트리가 일자로 연결된 경우 리프 노드의 부모를 찾기 위해서는 $N$개의 노드를 거쳐야 한다. 따라서 Find의 시간 복잡도는 $O(N)$이다. 정확히 말하면 쿼리당 $O(N)$이므로, Find를 M번 진행할 때 시간 복잡도는 $O(NM)$이다.
문제에서 쿼리는 최대 100,000개이고, 100,000개의 노드를 일렬로 연결하는 쿼리가 주어진다고 가정하면 당연히 TLE를 받는다.
아래의 두 테크닉을 통해 시간 복잡도를 $O(α(N))$으로 줄일 수 있다.
Path Compression
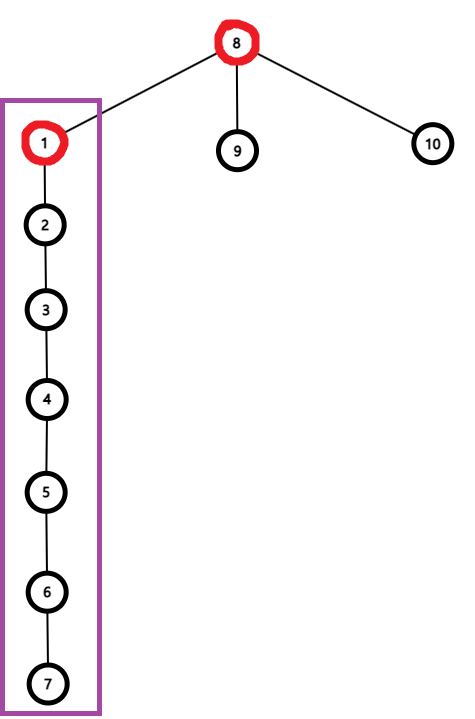
Path Compression은 Find를 실행할 때마다 트리를 평평하게(높이를 낮게)만드는 방법이다. 임의의 노드에서 루트 노드까지 순회중 방문한 각 노드들이 직접 루트 노드를 가리키도록 갱신하면 된다.
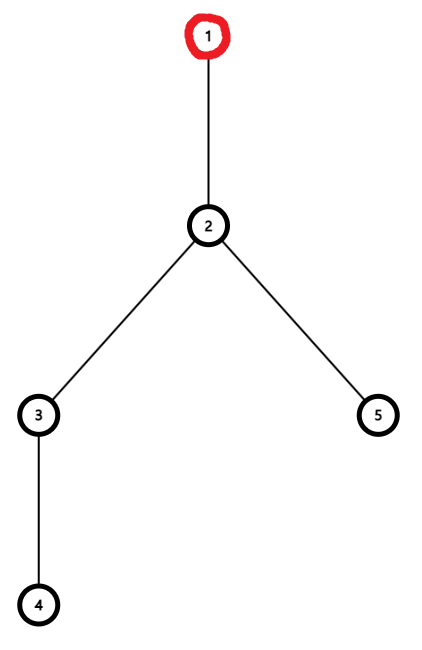
위와 같은 집합이 존재할 때, Path Compression을 적용하지 않는 경우, Find를 할 때마다 최대 $O(N)$의 시간 복잡도로 루트 노드까지 이동해야 한다.
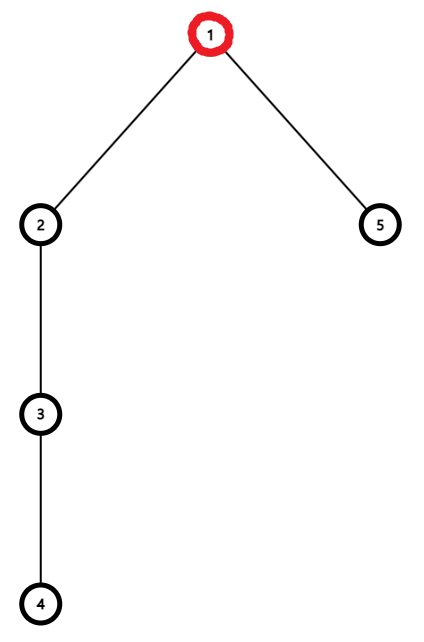
하지만 Path Compression을 적용하면 시간 복잡도를 줄일 수 있다. 위의 그림은 5번 노드에 대해 Path Compression을 적용한 Find를 실행한 후 그래프의 모습이다.
모든 노드에 대해 Find를 실행한 후 그래프의 모습이다. 모든 자식 노드들이 직접 루트 노드를 가리키고 있다.
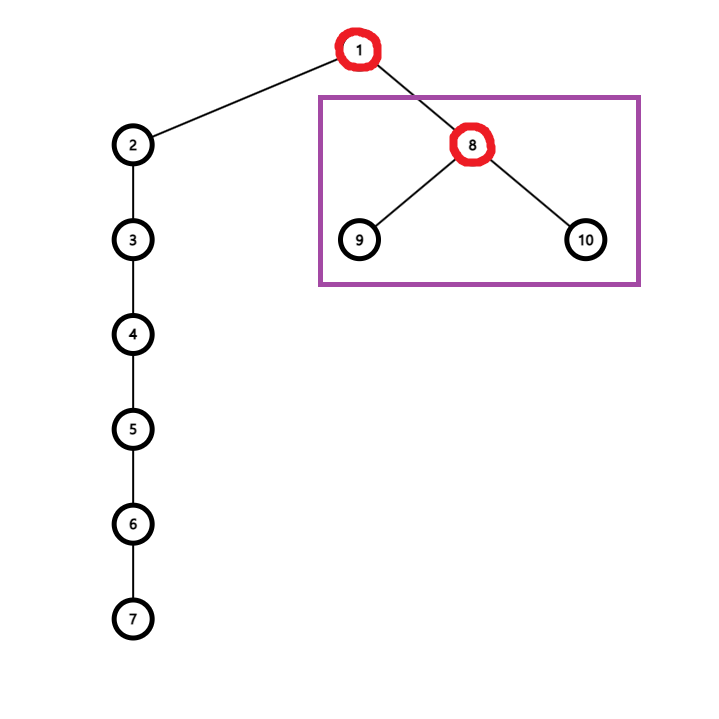
Union by Rank
Union by Rank는 Union에 적용되는 최적화로, 사이즈가 작은(혹은 높이가 낮은)트리를 사이즈가 큰(혹은 높이가 높은)트리에 합치는 것이다.
위의 두 집합에 대해 Union을 해보자.
큰 트리를 작은 트리에 합치는 경우 Find를 할 때 큰 트리의 노드의 개수만큼 탐색을 해야 한다. 다시 말해 Path Compression의 대상이 되는 노드가 많아진다는 뜻이다.
하지만 작은 트리를 큰 트리에 합치는 경우 전자의 경우보다 탐색 횟수가 적으므로 시간 단축이 가능하다.
두 최적화를 모두 적용할 경우 Find의 시간 복잡도는 $O(α(N))$이며, $α(N)$은 아커만 함수라고 한다. 결론적으로 상수 시간 복잡도를 가진다.
최적화된 구현
위 문제와 동일한 1717번: 집합의 표현의 코드이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include <bits/stdc++.h>
#define FastIO ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define ll long long
using namespace std;
int n, m;
int parent[1000001];
int treeSize[1000001];
int Find(int cur) {
if(parent[cur] == cur) {
return cur;
}
// Path Compression
return parent[cur] = Find(parent[cur]);
}
void Union(int a, int b) {
a = Find(a);
b = Find(b);
if(a == b) {
return;
}
// Union by Rank
if(treeSize[a] <= treeSize[b]) {
parent[a] = b;
treeSize[b] += treeSize[a];
}
else {
parent[b] = a;
treeSize[a] += treeSize[b];
}
}
void Query() {
int q, a, b;
for(int i = 0; i < m; i++) {
cin >> q >> a >> b;
if(q == 0) {
Union(a, b);
}
else {
if(Find(a) == Find(b)) {
cout << "YES" << '\n';
}
else {
cout << "NO" << '\n';
}
}
}
}
void Init() {
for(int i = 0; i <= n; i++) {
parent[i] = i;
treeSize[i] = 1;
}
}
void Solve() {
Init();
Query();
}
void Input() {
cin >> n >> m;
}
int main() {
FastIO;
Input();
Solve();
}